题目内容
过点A(1,4),且纵横截距的绝对值相等的直线共有 条.
分析:根据直线纵横截距的绝对值相等,分别讨论截距等于0和截距不等于0时对应的直线方程即可得到结论.
解答:解:∵直线的纵横截距的绝对值相等,
∴当直线过原点时,满足条件,此时设过原点的直线为y=kx,
∵直线过点A,
∴4=k,即此时直线方程为y=4x,
当直线不过原点,
则直线的截距时方程为
+
=1,
∵直线的纵横截距的绝对值相等,
∴|a|=|b|,
即b=a,或b=-a,
当b=a时,直线方程为x+y=a,
∵直线过点A,∴a=1+4=5,此时直线方程为x+y=5.
当b=-a时,直线方程为x-y=a,
∵直线过点A,∴a=1-4=-3,此时直线方程为x-y=-3.
∴满足条件的直线有3条.
故答案为:3.
∴当直线过原点时,满足条件,此时设过原点的直线为y=kx,
∵直线过点A,
∴4=k,即此时直线方程为y=4x,
当直线不过原点,
则直线的截距时方程为
| x |
| a |
| y |
| b |
∵直线的纵横截距的绝对值相等,
∴|a|=|b|,
即b=a,或b=-a,
当b=a时,直线方程为x+y=a,
∵直线过点A,∴a=1+4=5,此时直线方程为x+y=5.
当b=-a时,直线方程为x-y=a,
∵直线过点A,∴a=1-4=-3,此时直线方程为x-y=-3.
∴满足条件的直线有3条.
故答案为:3.
点评:本题主要考查直线的方程的确立,根据直线截距之间的关系建立条件关系即可,要注意截距为0时,也满足条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
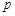 且
且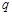 ”为假命题,则
”为假命题,则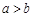 ,则
,则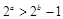 ”的否命题为“若
”的否命题为“若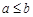 ,则
,则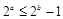 ”;
”;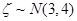 ,且
,且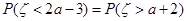 ,则
,则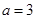 ;
;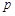 且
且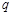 ”为假命题,则
”为假命题,则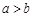 ,则
,则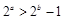 ”的否命题为“若
”的否命题为“若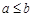 ,则
,则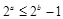 ”;
”;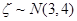 ,且
,且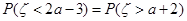 ,则
,则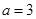 ;
;