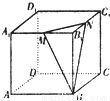
题目内容
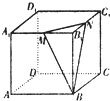 如图,在棱长为2a的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、B1C1的中点,则点C到面BMN的距离为
如图,在棱长为2a的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、B1C1的中点,则点C到面BMN的距离为分析:欲求点C到面BMN的距离,根据三棱锥C-MNB的体积公式可求得.
解答:解:设点C到面BMN的距离d,根据三棱锥的体积公式得:
VC-MNB=VM-NBC
∴
×
a×
ah=
×
×2a×2a×a
∴h=
.
故答案为:
.
VC-MNB=VM-NBC
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| 4a |
| 3 |
故答案为:
| 4a |
| 3 |
点评:本题主要考查了点、线、面间的距离计算以及空间想象能力、等价转化的能力,属于基础题.

练习册系列答案
相关题目
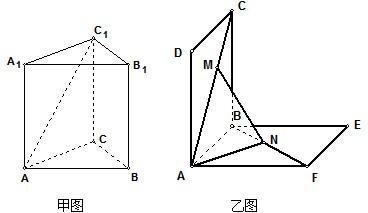
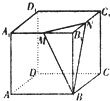 如图,在棱长为2a的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、B1C1的中点,则点C到面BMN的距离为________.
如图,在棱长为2a的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、B1C1的中点,则点C到面BMN的距离为________.