题目内容
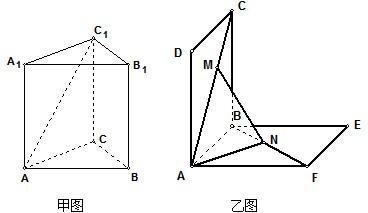
选做题:(甲、乙两题任选一题作答)甲、如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
| 2 |
(Ⅰ)建立适当的坐标系,并写出点A、B、A1、C1的坐标;
(Ⅱ)求AC1与侧面ABB1A1所成的角
乙、如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
| 2 |
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
分析:甲、(I)由题意及图形建立空间直角坐标系,得出点的坐标;
(II)利用向量知识得到MC1⊥面ABB1A1,在有线面角的定义,在三角形中得到所求的线面角的大小
乙、(I)由题意作MP∥AB交BC于点P,利用条件可以得到MNQP是平行四边形,进而求得求MN的长;
(II)由(I),利用二次函数求出线段MN的长取最值时的a的值及此时M,N的位置;
(III)取中点,利用等腰三角形得到垂直,利用二面角平面角的定义得到二面角的平面角,然后再三角形中解出角的大小即可.
(II)利用向量知识得到MC1⊥面ABB1A1,在有线面角的定义,在三角形中得到所求的线面角的大小
乙、(I)由题意作MP∥AB交BC于点P,利用条件可以得到MNQP是平行四边形,进而求得求MN的长;
(II)由(I),利用二次函数求出线段MN的长取最值时的a的值及此时M,N的位置;
(III)取中点,利用等腰三角形得到垂直,利用二面角平面角的定义得到二面角的平面角,然后再三角形中解出角的大小即可.
解答: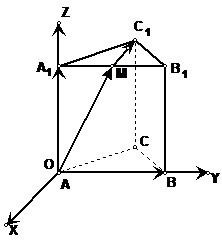 甲、解:(1)如图,以点A为坐标原点O,
甲、解:(1)如图,以点A为坐标原点O,
以AB所在直线为Oy轴,以AA1所在直线为Oz轴,
以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知,得A(0,0,0),B(0,a,0),
A1(0,0,
a),C1(-
a,
,
a)
(2)坐标系如上.取A1B1的中点M,
于是有M(0,
,
a),
连AM,MC1有
=(-
a,0,0),
且
=(0,a,0),
=(0,0,
a)
由于
•
=0,
•
=0
所以,MC1⊥面ABB1A1
∴AC1与AM所成的角就是AG1与侧面ABB1A1所成的角.
∵
=(-
a,
,
a),
=( 0,
,
a)
∴
•
=0+
+2a2=
a2
而|
|=
=
a
|
|=
=
a
∴cos<
,
>=
=
所以,
与
所成的角,
即AC1与侧面ABB1A1所成的角为30°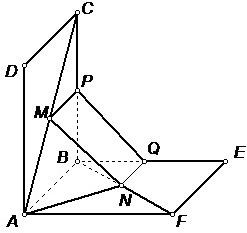
乙、解:(1)作MP∥AB交BC于点P,
NQ∥AB交BE于点Q,连接PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形.
∴MN=PQ由已知,CM=BN=a,CB=AB=BE=1,
∴
即CP=BQ=
∴MN=PQ=
=
=
(0<a<
)
(2)由(1)MN=
所以,当a=
时,MN=
即M,N分别移动到AC,BF的中点时,
MN的长最小,最小值为
(3)取MN的中点G,连接AG、BG,
∵AM=AN,BM=BN,∴AG⊥MN,BG⊥MN,
∴∠AGB即为二面角α的平面角.
又AG=BG=
,
所以由余弦定理有cosα=
=-
.
故所求二面角α=arccos(-
).
 甲、解:(1)如图,以点A为坐标原点O,
甲、解:(1)如图,以点A为坐标原点O,以AB所在直线为Oy轴,以AA1所在直线为Oz轴,
以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知,得A(0,0,0),B(0,a,0),
A1(0,0,
| 2 |
| ||
| 2 |
| a |
| 2 |
| 2 |
(2)坐标系如上.取A1B1的中点M,
于是有M(0,
| a |
| 2 |
| 2 |
连AM,MC1有
| MC1 |
| ||
| 2 |
且
| AB |
| AA1 |
| 2 |
由于
| MC1 |
| AA1 |
| MC1 |
| AA1 |
所以,MC1⊥面ABB1A1
∴AC1与AM所成的角就是AG1与侧面ABB1A1所成的角.
∵
| AC1 |
| ||
| 2 |
| a |
| 2 |
| 2 |
| AM |
| a |
| 2 |
| 2 |
∴
| AC1 |
| AM |
| a2 |
| 4 |
| 9 |
| 4 |
而|
| AC1 |
|
| 3 |
|
| AM |
|
| 3 |
| 2 |
∴cos<
| AC1 |
| AM |
| ||||
|
| ||
| 2 |
所以,
| AC1 |
| AM |
即AC1与侧面ABB1A1所成的角为30°

乙、解:(1)作MP∥AB交BC于点P,
NQ∥AB交BE于点Q,连接PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形.
∴MN=PQ由已知,CM=BN=a,CB=AB=BE=1,
∴
|
即CP=BQ=
| a | ||
|
∴MN=PQ=
| (1-CP)2+BQ2 |
=
(1-
|
=
(a-
|
| 2 |
(2)由(1)MN=
(a-
|
所以,当a=
| ||
| 2 |
| ||
| 2 |
即M,N分别移动到AC,BF的中点时,
MN的长最小,最小值为
| ||
| 2 |
(3)取MN的中点G,连接AG、BG,
∵AM=AN,BM=BN,∴AG⊥MN,BG⊥MN,
∴∠AGB即为二面角α的平面角.
又AG=BG=
| ||
| 4 |
所以由余弦定理有cosα=
(
| ||||||||
2•
|
| 1 |
| 3 |
故所求二面角α=arccos(-
| 1 |
| 3 |
点评:甲:此题重点考查了利用条件恰当建立空间直角坐标系,写出点的坐标,还考查了利用向量证明线面垂直,还考查了线面角的知识;
乙:此题重点考查了学生的空间想象能力及方程的思想,还考查了由线线平行得三角形相似,进而线段成比例进而在三角形中解出MN的长,此时MN的长是用a表示的.还考查了利用一元二次函数的值域求出最小值及对应的M,N的位置,此外还考查了二面角的平面角的概念及在三角形中求解出角的大小及利用反三角函数表示角的大小.
乙:此题重点考查了学生的空间想象能力及方程的思想,还考查了由线线平行得三角形相似,进而线段成比例进而在三角形中解出MN的长,此时MN的长是用a表示的.还考查了利用一元二次函数的值域求出最小值及对应的M,N的位置,此外还考查了二面角的平面角的概念及在三角形中求解出角的大小及利用反三角函数表示角的大小.

练习册系列答案
相关题目
 .
. .
. .
.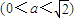 .
.
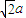 .
. .
.