题目内容

如图，正四棱锥S—ABCD的底面边长为a,侧棱长为2a,点P、Q分别在BD和SC上，并且BP∶PD=1∶2，PQ∥平面SAD，求线段PQ的长.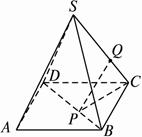

解析：延长CP交DA延长线于R.?

∵BC∥AD，∴.?

∵PQ∥面SAD，面CSR∩面ASD=RS，∴PQ∥RS.?

∴，DR=2BC=2a.?

∵SA=SD=2a,AD=a,?

∴cos∠SDA=.?

∴SR2=4a2+4a2-2a·2a·2·=6a2.?

∴SR=a.∴PQ=SR=.?


练习册系列答案
相关题目
精英家教网如图，正四棱锥S-ABCD中，E是侧棱SC的中点，异面直线SA和BC所成角的大小是60°．
（1）求证：直线SA∥平面BDE；
（2）求二面角A-SB-D的余弦值；
（3）求直线BD和平面SBC所成角的正弦值．
12、如图在正四棱锥S-ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC，则动点P的轨迹与△SCD组成的相关图形是（　　）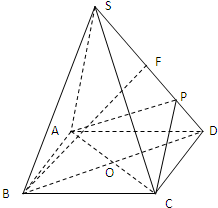
如图，正四棱锥S-ABCD 的底面是边长为a正方形，O为底面对角线交点，侧棱长是底面边长的
2
倍，P为侧棱SD上的点．
（Ⅰ）求证：AC⊥SD；
（Ⅱ）若SD⊥平面PAC，F为SD中点，求证：BF∥平面PAC；
（Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．
（2006•西城区二模）如图，正四棱锥S-ABCD中，E是侧棱SC的中点，异面直线SA和BC所成角的
大小是60°．
（1）求证：直线SA∥平面BDE；
（2）求二面角A-SB-D的大小；
（3）求直线BD和平面SBC所成角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网