题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F与长轴垂直的直线与椭圆在第一象限相交于点M,
,过右焦点F与长轴垂直的直线与椭圆在第一象限相交于点M,![]() .
.
(1)求椭圆C的标准方程;
(2)斜率为1的直线l与椭圆相交于B,D两点,若以线段BD为直径的圆恰好过坐标原点,求直线l的方程.
【答案】(1)![]() .(2) y=x
.(2) y=x![]() 或y=x
或y=x![]() .
.
【解析】
(1)根据离心率![]() 得到a2=2 c2,根据
得到a2=2 c2,根据![]() 得到
得到![]() ,计算得到答案.
,计算得到答案.
(2)设 l 的方程为:y=x+m,B(x1,y1),D(x2,y2),联立方程,利用韦达定理得到x1+x2![]() ,x1 x2
,x1 x2![]() ,代入计算
,代入计算![]() 得到答案.
得到答案.
(1)∵椭圆的离心率为![]() ,∴e
,∴e![]() ,即a2=2c2①,
,即a2=2c2①,
∵过右焦点F与长轴垂直的直线与椭圆在第一象限相交于点M,![]() .
.
∴M(c,![]() )再代入椭圆方程得,
)再代入椭圆方程得,![]() ②,又a2=b2+c2③,
②,又a2=b2+c2③,
联立①②③得,b2=c2=1,a2=2,∴椭圆方程:![]() .
.
(2)设 l 的方程为:y=x+m,B(x1,y1),D(x2,y2),
联立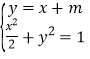 ,得3x2+4mx+2m2﹣2=0,
,得3x2+4mx+2m2﹣2=0,
x1+x2![]() ,x1 x2
,x1 x2![]() ,y1+y2
,y1+y2![]() ,y1 y2
,y1 y2![]() ,
,
∵以线段BD为直径的圆恰好过坐标原点,
∴![]() 0,
0,
∴m![]() .
.
∴直线l方程为 y=x![]() 或y=x
或y=x![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目