题目内容
已知恒过定点(1,1)的圆C截直线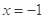 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )
A.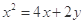 | B.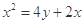 |
C.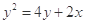 | D.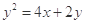 |
D
解析试题分析:设圆心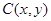 ,则
,则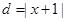 ,
,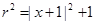 ,则满足
,则满足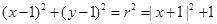 ,
,
∴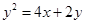 .
.
考点:1.轨迹求解问题;2.直线与圆相交形成弦问题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知平面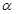 ∥平面
∥平面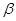 ,点P
,点P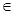 平面
平面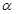 ,平面
,平面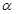 、
、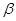 间的距离为8,则在
间的距离为8,则在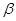 内到点P的距离为10的点的轨迹是( )
内到点P的距离为10的点的轨迹是( )
| A.一个圆 | B.四个点 |
| C.两条直线 | D.两个点 |
曲线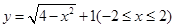 与直线
与直线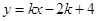 有两个不同的交点时,实数k的取值范围是 ( )
有两个不同的交点时,实数k的取值范围是 ( )
A.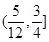 | B.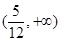 | C.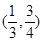 | D. |
已知点 是圆
是圆 上任意一点,
上任意一点, 点关于直线
点关于直线 的对称点在圆上,则实数
的对称点在圆上,则实数 等于( )
等于( )
A. | B. | C. | D.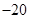 |
直线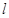 过点
过点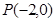 且与圆
且与圆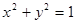 相切,则
相切,则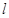 的斜率是( )
的斜率是( )
A. ; ; | B.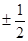 ; ; | C.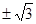 ; ; | D.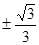 . . |
已知实数 是常数,如果
是常数,如果 是圆
是圆 外的一点,那么直线
外的一点,那么直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.都有可能 |
若直线 与曲线
与曲线 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )
A.[ , , ] ] | B.[ ,3] ,3] |
C.[-1, ] ] | D.[ ,3]; ,3]; |
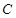 :
: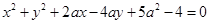 上所有的点均在第二象限内,则实数
上所有的点均在第二象限内,则实数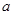 的取值范围为( )
的取值范围为( )
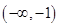
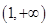
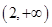
 与圆
与圆 的位置关系为( )
的位置关系为( )