题目内容
已知点
是圆
上任意一点，点关于直线
的对称点在圆上，则实数
等于( )
A． | B． | C． | D． |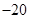
B
解析试题分析：将圆化成标准方程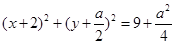
，故圆心为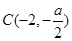
，依意可知直线过点圆心
，所以
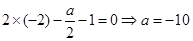，故选B.
考点：1.圆的方程；2.直线与圆的位置关系.
练习册系列答案
特高级教师点拨系列答案
相关题目
若圆
关于直线
和直线
都对称，则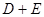
的值为（ ）
A． | B． | C． | D． |
若点
为圆
的弦
的中点，则弦所在直线方程为( )
A． | B． |
C． | D． |
已知圆的方程为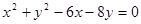
，过点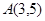
的直线被圆所截，则截得的最短弦的长度为 ( ).
A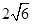． | B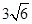． | C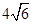． | D． |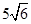
过点
作圆
的两条切线，切点分别为
，
，则直线
的方程为（ ）
| A．2x+y-3=0 | B．2x-y-3="0" | C．4x-y-3=0 | D．4x+y-3=0 |
已知恒过定点(1,1)的圆C截直线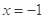
所得弦长为2，则圆心C的轨迹方程为( )
A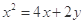． | B． |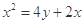
C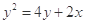． | D． |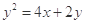
过点P（0,1）与圆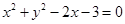
相交的所有直线中，被圆截得的弦最长时的直线方程是（ ）
A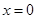． | B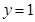． | C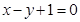． | D． |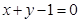
与圆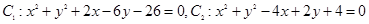
都相切的直线有（ ）
| A．1条 | B．2条 | C．3条 | D．4条 |
