题目内容
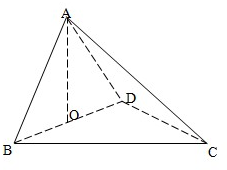如图，四面体ABCD中，△ABD和△BCD均为等边三角形，BD=2，O是BD的中点，且AO⊥平面BCD．（1）求二面角A-BC-D的大小（结果用反三角函数表示）；
（2）求点O到平面ACD的距离．
分析：（1）以O为原点，OB、OC、OA所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，分别求出平面BCD，面ABC的一个法向量，利用两个发向量夹角求解．
（2）求出平面ACD的一个法向量
，点O到平面ACD的距离 为
在
方向上投影的绝对值．
（2）求出平面ACD的一个法向量
| m |
| AO |
| m |
解答：解：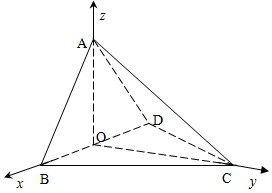
（1）因为△ABD和△BCD都是等边三角形，O是BD中点，所以AO⊥BD，CO⊥BD，以O为原点，OB、OC、OA所在直线分别为x轴、y轴、z轴，建立空间直角坐标系．…（1分）
则O（0，0，0），A(0，0，
)，B（1，0，0），C(0，
，0)，D（-1，0，0），…（2分）
因为AO⊥平面BCD，所以平面BCD的一个法向量为
=(0，0，
)，…（3分）
=(1，0，-
)，
=(-1，
，0)，
设平面ABC的一个法向量为
=(x，y，z)，
则
⊥
，
⊥
，所以
•
=0，
•
=0，
即
，令z=1，得x=
，y=1，所以
=(
，1，1)，…（5分）
设
与
的夹角为θ，则cosθ=
=
=
，…（6分）
由图形可知，二面角A-BC-D为锐角，
所以二面角A-BC-D的大小为arccos
．…（7分）
（2）设平面ACD的一个法向量为
=(u，v，w)，则
⊥
，
⊥
，
又
=(1，0，
)，
=(1，
，0)，…（8分）
所以，由
，得
，令u=-
，则v=1，w=1，
故
=(-
，1，1)，…（10分）
因为
•
=
，|
|=
，…（12分）
所以点O到平面ACD的距离为
=
=
．…（14分）
（1）因为△ABD和△BCD都是等边三角形，O是BD中点，所以AO⊥BD，CO⊥BD，以O为原点，OB、OC、OA所在直线分别为x轴、y轴、z轴，建立空间直角坐标系．…（1分）则O（0，0，0），A(0，0，
| 3 |
| 3 |
因为AO⊥平面BCD，所以平面BCD的一个法向量为
| OA |
| 3 |
| AB |
| 3 |
| BC |
| 3 |
设平面ABC的一个法向量为
| n |
则
| n |
| AB |
| n |
| BC |
| n |
| AB |
| n |
| BC |
即
|
| 3 |
| n |
| 3 |
设
| OA |
| n |
| ||||
|
|
| ||||
|
| ||
| 5 |
由图形可知，二面角A-BC-D为锐角，
所以二面角A-BC-D的大小为arccos
| ||
| 5 |
（2）设平面ACD的一个法向量为
| m |
| m |
| DA |
| m |
| DC |
又
| DA |
| 3 |
| DC |
| 3 |
所以，由
|
|
| 3 |
故
| m |
| 3 |
因为
| OA |
| m |
| 3 |
| m |
| 5 |
所以点O到平面ACD的距离为
|
| ||||
|
|
| ||
|
| ||
| 5 |
点评：本题考查二面角、空间距离大小计算．考查空间想象能力、逻辑思维能力和运算能力．
练习册系列答案
口算能手系列答案
相关题目
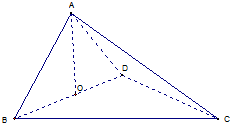如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，
如图，四面体ABCD中，0是BD的中点，CA=CB=CD=BD=a，AB=AD=
如图，四面体ABCD的各个面都是直角三角形，已知AB⊥BC，BC⊥CD，AB=a，BC=a，CD=c．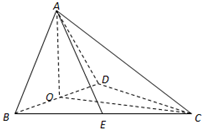
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．