题目内容
如图,四面体ABCD中,O.E分别为BD.BC的中点,且CA=CB=CD=BD=2,AB=AD=| 2 |
(1)求证:AO⊥平面BCD;
(2)求 异面直线AB与CD所成角的余弦值.
分析:(1)如图所示,要证AO⊥平面BCD,只需证AO⊥BD,AO⊥CO即可,用运算的方式来证明结论.
(2)取AC中点F,连接OF.OE.EF,由中位线定理可得EF∥AB,OE∥CD所以∠OEF(或其补角)是异面直线AB与CD所成角,然后在Rt△AOC中求解.
(2)取AC中点F,连接OF.OE.EF,由中位线定理可得EF∥AB,OE∥CD所以∠OEF(或其补角)是异面直线AB与CD所成角,然后在Rt△AOC中求解.
解答: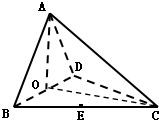 解:(1)证明:△ABD中
解:(1)证明:△ABD中
∵AB=AD=
,O是BD中点,BD=2
∴AO⊥BD且AO=
=1
△BCD中,连接OC∵BC=DC=2
∴CO⊥BD且CO=
=
△AOC中AO=1,CO=
,AC=2
∴AO2+CO2=AC2故AO⊥CO
∴AO⊥平面BCD
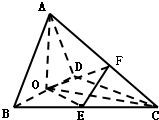 (2)取AC中点F,连接OF.OE.EF
(2)取AC中点F,连接OF.OE.EF
△ABC中E.F分别为BC.AC中点
∴EF∥AB,且EF=
AB=
△BCD中O.E分别为BD.BC中点
∴OE∥CD且OE=
CD=1
∴异面直线AB与CD所成角等于∠OEF(或其补角)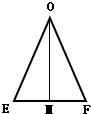
又OF是Rt△AOC斜边上的中线∴OF=
AC=1
∴等腰△OEF中cos∠OEF=
=
 解:(1)证明:△ABD中
解:(1)证明:△ABD中∵AB=AD=
| 2 |
∴AO⊥BD且AO=
| AB2-BO2 |
△BCD中,连接OC∵BC=DC=2
∴CO⊥BD且CO=
| BC2-BO2 |
| 3 |
△AOC中AO=1,CO=
| 3 |
∴AO2+CO2=AC2故AO⊥CO
∴AO⊥平面BCD
 (2)取AC中点F,连接OF.OE.EF
(2)取AC中点F,连接OF.OE.EF△ABC中E.F分别为BC.AC中点
∴EF∥AB,且EF=
| 1 |
| 2 |
| ||
| 2 |
△BCD中O.E分别为BD.BC中点
∴OE∥CD且OE=
| 1 |
| 2 |
∴异面直线AB与CD所成角等于∠OEF(或其补角)

又OF是Rt△AOC斜边上的中线∴OF=
| 1 |
| 2 |
∴等腰△OEF中cos∠OEF=
| ||
| OE |
| ||
| 4 |
点评:本题主要考查线线,线面,面面垂直的转化及异面直线所成角的求法,同时,考查了转化思想和运算能力,是常考类型,属中档题.

练习册系列答案
相关题目
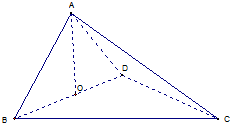 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.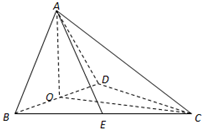 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.