题目内容
 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.(1)若AC⊥CD,求证:AB⊥BD;
(2)求四面体ABCD的表面积.
分析:(1)由题意可得:CD⊥平面ABC,再根据面面垂直的判断定理可得:平面ABC⊥平面BCD,进而得到线面垂直得到线线垂直.
(2)此题分情况讨论:当AC⊥CD时,则AB⊥BD,进而得到四面体ABCD的表面积.当AC与CD不垂直时,则AD⊥CD,当AD⊥AC时,再讨论AB与AD不能垂直,并且BD与AD不能垂直,进而得到AB⊥BD得到答案.
(2)此题分情况讨论:当AC⊥CD时,则AB⊥BD,进而得到四面体ABCD的表面积.当AC与CD不垂直时,则AD⊥CD,当AD⊥AC时,再讨论AB与AD不能垂直,并且BD与AD不能垂直,进而得到AB⊥BD得到答案.
解答:解:(1)因为AC⊥CD,BC⊥CD,
所以CD⊥平面ABC,
又因为CD?平面BCD,
所以平面ABC⊥平面BCD,
因为AB⊥BC,平面ABC∩平面BCD=BC,
所以AB⊥平面BCD,
所以AB⊥BD.
(2)当AC⊥CD时,则AB⊥BD,
因为AB=a,BC=b,CD=c,
所以BD=
,AC=
,
所以四面体ABCD的表面积S=
ab+
bc+
a
+
c
.
当AC与CD不垂直时,则AD⊥CD,否则由(1)知AB⊥BD,可得AC⊥CD(矛盾),
当AD⊥AC时,AB与AD不能垂直,否则AD⊥平面ABC,
所以BC⊥AD,
因为BC⊥CD,BC⊥平面ACD,
所以BC⊥AC,这与AB⊥BC矛盾,
所以BD⊥AD,从而可得:AD2=a2-b2-c2,…①
由AD⊥AC得,AD2=c2-b2-a2…②
由①②可得:a=c,所以AD2=-b2<0矛盾.
所以AD⊥CD,从而得到AB⊥AD,
当AD⊥CD时,AD2=a2+b2-c2,
当AB⊥AD时,AD2=b2+c2-a2,
所以a=c,AD=b,此时四面体的各个面是全等的三角形,变形成为一平面图形,所以舍去.
所以其表面积为S=
ab+
bc+
a
+
c
.…12(分)
所以CD⊥平面ABC,
又因为CD?平面BCD,
所以平面ABC⊥平面BCD,
因为AB⊥BC,平面ABC∩平面BCD=BC,
所以AB⊥平面BCD,
所以AB⊥BD.
(2)当AC⊥CD时,则AB⊥BD,
因为AB=a,BC=b,CD=c,
所以BD=
| b2+c2 |
| a2+b2 |
所以四面体ABCD的表面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b2+c2 |
| 1 |
| 2 |
| a2+b2 |
当AC与CD不垂直时,则AD⊥CD,否则由(1)知AB⊥BD,可得AC⊥CD(矛盾),
当AD⊥AC时,AB与AD不能垂直,否则AD⊥平面ABC,
所以BC⊥AD,
因为BC⊥CD,BC⊥平面ACD,
所以BC⊥AC,这与AB⊥BC矛盾,
所以BD⊥AD,从而可得:AD2=a2-b2-c2,…①
由AD⊥AC得,AD2=c2-b2-a2…②
由①②可得:a=c,所以AD2=-b2<0矛盾.
所以AD⊥CD,从而得到AB⊥AD,
当AD⊥CD时,AD2=a2+b2-c2,
当AB⊥AD时,AD2=b2+c2-a2,
所以a=c,AD=b,此时四面体的各个面是全等的三角形,变形成为一平面图形,所以舍去.
所以其表面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b2+c2 |
| 1 |
| 2 |
| a2+b2 |
点评:本题主要考查空间中的点、线、面得位置关系,解决此类问题的关键是熟练掌握线面垂直、线线垂直、面面垂直的判定定理与性质定理,此题考查学生的推理论证与空间想象能力,以及考查分析问题与解决问题的能力,此题考查的知识比较基础,但象这种基础知识也是学生的薄弱点与易错点.

练习册系列答案
相关题目
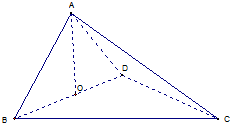 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=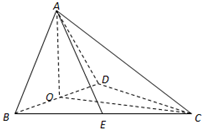 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.