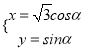��Ŀ����
����Ŀ��ij�����ij���ǿ��ٳ����������٣�Ϊ�˵��иõ�·�����������ij��ʱ�������![]() �������ٶȽ���ȡ���������ij����Ƴ���������ͼ��
�������ٶȽ���ȡ���������ij����Ƴ���������ͼ��
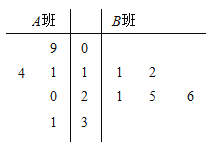
�����㣺������ƽ��ֵ![]() ������
������![]() ����Ƶ��ֵ��Ϊ���ʵĹ���ֵ.��֪���ٹ�������춼����Ϊ��������ٶȣ��ֹ涨����С��
����Ƶ��ֵ��Ϊ���ʵĹ���ֵ.��֪���ٹ�������춼����Ϊ��������ٶȣ��ֹ涨����С��![]() ���ٴ���
���ٴ���![]() ��������ٶ�.
��������ٶ�.
��1���Ӹÿ��ٳ��������г�������ȡ![]() ������ó�����������ٶȵĸ��ʣ�
������ó�����������ٶȵĸ��ʣ�
��2������������ȡ![]() ������������
������������![]() ����������������ٶȵĸ��ʣ�
����������������ٶȵĸ��ʣ�
��3���Ӹÿ��ٳ��������г�������ȡ![]() ������������������ٶȵĸ���Ϊ
������������������ٶȵĸ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡�(1) ![]() ;(2 )
;(2 ) ![]() ;(3)������.
;(3)������.
�������������������1�����¼�![]() Ϊ���Ӹÿ��ٳ��������г�������ȡ
Ϊ���Ӹÿ��ٳ��������г�������ȡ![]() �����ó�����������ٶ��������ݸ���������ͼ����������¼�
�����ó�����������ٶ��������ݸ���������ͼ����������¼�![]() �ĸ��ʣ�
�ĸ��ʣ�
��2�����¼�![]() Ϊ������������ȡ
Ϊ������������ȡ![]() ����������
����������![]() ����������������ٶ����������裬���ùŵ���ͼ�����ʵļ��㹫ʽ����������¼�
����������������ٶ����������裬���ùŵ���ͼ�����ʵļ��㹫ʽ����������¼�![]() ���ʣ�
���ʣ�
��3��������ã�������ٶȵĸ���![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ���������
���������![]() ��Ӧ�ĸ��ʣ��г��ֲ��У�������ѧ������
��Ӧ�ĸ��ʣ��г��ֲ��У�������ѧ������
�����������1�����¼�![]() Ϊ���Ӹÿ��ٳ��������г�������ȡ
Ϊ���Ӹÿ��ٳ��������г�������ȡ![]() �����ó�����������ٶ�����
�����ó�����������ٶ�����
��Ϊ![]() ��
��
����������ͼ��֪������ĸ���Ϊ
![]() .
.
��2�����¼�![]() Ϊ������������ȡ
Ϊ������������ȡ![]() ����������
����������![]() ����������������ٶ���
����������������ٶ���
�������֪��������Ϊ![]() ����������ٶȸ���Ϊ
����������ٶȸ���Ϊ![]() �������������Ϊ
�������������Ϊ![]() .
.
��3��������ٶȵĸ���![]() ���Ӷ���ֲ�����
���Ӷ���ֲ�����![]() ��
��
��![]() ��
�� ![]() ��
��
![]() ��
��
���![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
��![]() ��֪��ѧ����
��֪��ѧ����![]() .
.

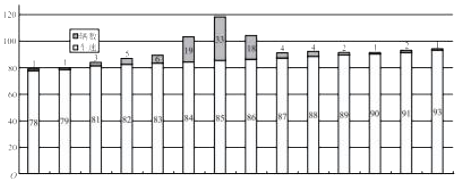
����Ŀ�����ھ�������Խ��Խ�࣬������ѧ��Ҳ�����˾����������˻��������빤�������ʽ�йأ�ij�������Ϊ���˽��ѧ�����о����Ƿ��볤�ڹ���ʹ�õ��Ӳ�Ʒ�йأ�������������ҽԺ����Ķ���Ժ��50����ѧ���������ʾ����飬�õ������µ�4��4��������
δ����ʹ�� | ����ʹ�� | �ϼ� | |
����� | 15 | 5 | 20 |
������ | 10 | 20 | 30 |
�ϼ� | 25 | 25 | 50 |
��1���Ƿ���99.5%�İ�����Ϊ��ѧ���������볤�ڹ���ʹ�õ��Ӳ�Ʒ�йأ�
��2����֪�ڻ��о�����10��δ����ʹ�õ��Ӳ�Ʒ�Ĵ�ѧ���У���3����ѧ���ֻ��г�θ�ף����ڴ�������10����ѧ���У���ȡ3����ѧ����������������Ų飬��ѡ������θ��ѧ������Ϊ![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
�ο������빫ʽ��
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
����Ŀ��ij����2008����2014���У�ÿ��ľ����˾�������y����λ��ǧԪ�����������±���
�� �� | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
��ݴ���t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
�Ա���t��y��������Լ��飬��֪t��y֮�����������ع�ϵ��
��1����y����t�����Իع鷽�̣�
��2��Ԥ��õ���2017��ľ����˾������룮
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
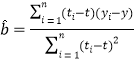 ��
��![]()