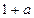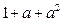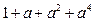题目内容
已知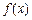 是定义在
是定义在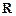 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的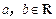 都满足:
都满足: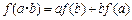 ,若
,若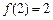 ,
,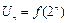 (
(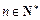 ),求证:
),求证: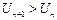 .
.
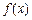 是定义在
是定义在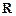 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的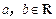 都满足:
都满足: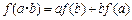 ,若
,若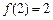 ,
,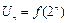 (
(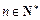 ),求证:
),求证: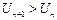 .
.证明见解析
证明:令
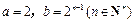 ,
,当
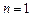 时,
时,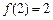 ;当
;当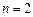 时,
时,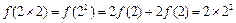 ;
;当
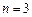 时,
时,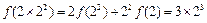 ;
;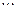
猜想
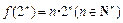 ,
, 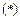
用数学归纳法证明如下:
(1) 当
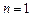 时,
时,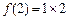 ,
,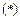 式成立,
式成立,(2) 假设
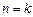 时,
时,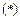 式成立,即
式成立,即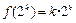 ,当
,当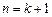 时,
时,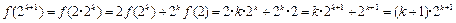 ,
,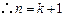 时,
时,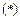 式成立.
式成立.由(1)(2)知,对
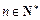 ,
,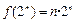 成立,
成立,所以
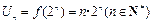 .
.要证明结论成立,只需证明
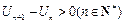 ,
,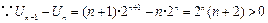 ,
,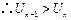 .
.
练习册系列答案
相关题目
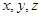 满足
满足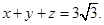
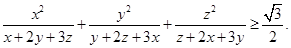
 的最小值.
的最小值.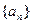 满足
满足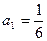 ,前n项和
,前n项和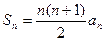
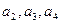 ;(2)猜出
;(2)猜出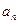 的表达式,并用数学归纳法证明
的表达式,并用数学归纳法证明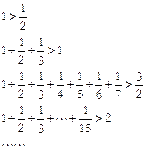
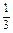 )(1+
)(1+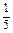 )…(1+
)…(1+ )>
)>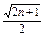 均成立.
均成立.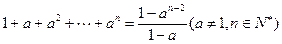 ,在验证n=1时,左边计算所得的式子是()
,在验证n=1时,左边计算所得的式子是()