题目内容
一批灯泡400只,其中20 W、40 W、60 W的数目之比为4∶3∶1,现用分层抽样的方法产生一个容量为40的样本,三种灯泡依次抽取的个数为( )
| A.20 ,10 , 10 | B.15 , 20 , 5 | C.20, 5, 15 | D.20, 15, 5 |
D
解析试题分析:根据题意,由于一批灯泡400只,其中20 W、40 W、60 W的数目之比为4∶3∶1,那么可知各层所抽取的应该分别是 ,故选D.
,故选D.
考点:分层抽样
点评:解决的关键是对属于分层抽样的等比例性的运用,属于基础题。

练习册系列答案
相关题目
为了了解某地区高三学生的身体素质情况,抽查了该地区 名年龄为17.5岁-18岁的男生体重(
名年龄为17.5岁-18岁的男生体重( ) ,得到频率分布直方图如下
) ,得到频率分布直方图如下
根据上图可得这 名学生中体重在[56.5,64.5]的学生人数是( )
名学生中体重在[56.5,64.5]的学生人数是( )
A. | B.30 | C. | D.50 |
对变量x,y观测数据(x1,y1)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u1,v1)(i=1,2,…,10),得散点图2.由这两个散点图可以判断.( )
| A.变量x与y正相关,u与v正相关 |
| B.变量x与y正相关,u与v负相关 |
| C.变量x与y负相关,u与v正相关 |
| D.变量x与y负相关,u与v负相关 |
工人月工资(元)依劳动产值(千元)变化的回归直线方程为 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )
| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |
已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A. =1.23x+4 =1.23x+4 | B. =1.23x+5 =1.23x+5 | C. =1.23x+0.08 =1.23x+0.08 | D. =0.08x+1.23 =0.08x+1.23 |
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
| A.45,75,15 | B.45,45,45 |
| C.30,90,15 | D.45,60,30 |
若样本 +2,
+2, +2, ,
+2, , +2的平均数为10,方差为3,则样本2
+2的平均数为10,方差为3,则样本2 +3,2
+3,2 +3,… ,2
+3,… ,2 +3,
+3,
的平均数、方差、标准差是( )
A.19,12, | B.23,12, | C.23,18, | D.19,18, |
某中学从已编号(1~60)的60个班级中,随机抽取6个班级进行卫生检查,用每部分选取的号码间隔一样的系统抽样方法确定所选的6个班级的编号可能是( )
| A.6,16,26,36,46,56 | B.3,10,17,24,31,38 |
| C.4,11,18,25,32,39 | D.5,14,23,32,41,50 |
 =bx+a必过( )
=bx+a必过( ) B.点
B.点 C.点
C.点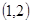 D.点
D.点