题目内容
17.已知圆C:x2+y2-2x+6y=0(a∈R)的圆心在直线2x-y+a=0上.(1)求实数a的值.
(2)求圆C与直线l:(2m+1)x+(m+1)y-m=0(m∈R)相交弦长最小值.
分析 (1)圆化为标准方程,求得圆心,代入直线2x-y+a=0,求出实数a的值.
(2)求出直线过定点(1,-1),可得圆心与定点的距离为2,即可求出弦长最小值.
解答 解:(1)圆C:x2+y2-2x+6y=0可化为(x-1)2+(y+3)2=10,圆心为(1,-3),半径为$\sqrt{10}$,
∵圆C:x2+y2-2x+6y=0的圆心在直线2x-y+a=0上,
∴2+3+a=0,
∴a=-5;
(2)直线l:(2m+1)x+(m+1)y-m=0(m∈R)可化为(2x+y-1)m+(x+y)=0,
∴$\left\{\begin{array}{l}{2x+y-1=0}\\{x+y=0}\end{array}\right.$,∴x=1,y=-1,即直线过定点(1,-1),
圆心与定点的距离为2,∴弦长最小值为2$\sqrt{10-4}$=2$\sqrt{6}$.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,求得直线过定点是关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
4.已知某空间几何体的三视图如图所示,则该几何体的体积是( )
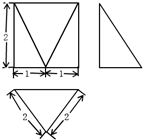

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |