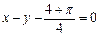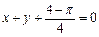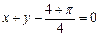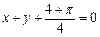题目内容
.曲线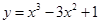 在点(1, -1)处的切线方程是 ( )
在点(1, -1)处的切线方程是 ( )
A y=3x-4 B y=-3x+2 C y=-4x+3 D y=4x-5
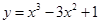 在点(1, -1)处的切线方程是 ( )
在点(1, -1)处的切线方程是 ( ) A y=3x-4 B y=-3x+2 C y=-4x+3 D y=4x-5
B
首先判断该点是否在曲线上,①若在曲线上,对该点处求导就是切线斜率,利用点斜式求出切线方程;②若不在曲线上,想法求出切点坐标或斜率.
解:∵点(1,-1)在曲线上,y′=3x2-6x,
∴y′|x=1=-3,即切线斜率为-3.
∴利用点斜式,切线方程为y+1=-3(x-1),即y=-3x+2.
故选B.
解:∵点(1,-1)在曲线上,y′=3x2-6x,
∴y′|x=1=-3,即切线斜率为-3.
∴利用点斜式,切线方程为y+1=-3(x-1),即y=-3x+2.
故选B.

练习册系列答案
相关题目
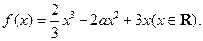
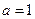 ,点P为曲线
,点P为曲线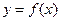 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;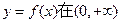 上为单调增函数,试求满足条件的最大整数a.
上为单调增函数,试求满足条件的最大整数a.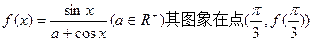 处的切线与直线
处的切线与直线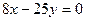 平行;
平行;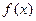 的单调区间;
的单调区间;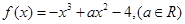
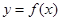 的图象在点
的图象在点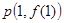 处的切线的倾斜角为
处的切线的倾斜角为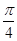 ,求
,求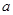
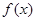 的导函数是
的导函数是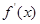 ,在(Ⅰ)的条件下,若
,在(Ⅰ)的条件下,若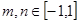 ,求
,求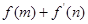 的最小值。
的最小值。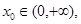 使
使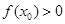 ,求
,求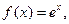 则
则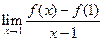 等于
等于 
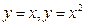 所围成图形的面积 。
所围成图形的面积 。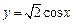 在
在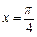 处的切线方程是
处的切线方程是