题目内容
【题目】已知
三个顶点到平面
的距离分别是3，3，6，则其重心到平面的距离为__________．（写出所有可能值）
【答案】0，2，4
【解析】
可将所有情况分为三类：①
在平面同侧，且
在平面另一侧；②
位于平面同侧，
在平面另一侧；③
在平面同侧；利用重心分中线成比例的性质可分别求得结果.
设到平面
距离为
；到平面距离为
①若在平面同侧，且在平面另一侧，则
取
中点
，连接
，设重心为
又到平面的距离
，到平面的距离
由重心性质可知：
到平面的距离为
②若位于平面同侧，在平面另一侧，取
中点，连接
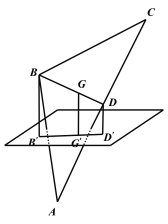
设重心为，
在平面内的射影分别为：
，如下图所示：
，
又
，即到平面距离为
③若在平面同侧，则，取中点，连接
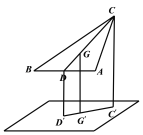
设重心为，
在平面内的射影分别为
，如下图所示：
，
又
，即到平面距离为
综上所述，重心到平面距离为
本题正确结果：
练习册系列答案
相关题目
【题目】总体由编号为01，02，03，
，49，50的50个个体组成，利用随机数表（以下选取了随机数表中的第1行和第2行）选取5个个体，选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取，则选出来的第4个个体的编号为（ ）
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20