题目内容
1.函数f(x)=lnx-$\frac{1}{2}$ax2-2x.(1)在[1,4]上是减函数,求a的范围;
(2)存在减区间,求a的范围.
分析 (1)问题转化为a>$\frac{1}{{x}^{2}}$-$\frac{2}{x}$在[1,4]恒成立,令h(x)=$\frac{1}{{x}^{2}}$-$\frac{2}{x}$,求出h(x)的最大值,从而求出a的范围即可;
(2)解法1:先求出函数f(x)的导数,问题转化为ax2+2x-1>0有正的实数解,由方程的观点去求解;
解法2:先求出函数f(x)的导数,问题转化为a>$\frac{1}{{x}^{2}}$-$\frac{2}{x}$在(0,+∞)内有实数解,求其值域即可.
解答 解:(1)f′(x)=$\frac{1}{x}$-ax-2=$\frac{1-{ax}^{2}-2x}{x}$,(x>0)
由题意可知f′(x)<0在[1,4]恒成立.
即1-ax2-2x<0在[1,4]恒成立
即a>$\frac{1}{{x}^{2}}$-$\frac{2}{x}$在[1,4]恒成立,
令h(x)=$\frac{1}{{x}^{2}}$-$\frac{2}{x}$,则h(x)=($\frac{1}{x}$-1)2-1≥-1,
而h(x)在[1,4]单调递减,h(x)max=h($\frac{1}{4}$)=-$\frac{7}{16}$,
∴a>-$\frac{7}{16}$;
(2)解法1:f′(x)=$\frac{1}{x}$-ax-2=$\frac{1-{ax}^{2}-2x}{x}$,
由题意知f′(x)<0有实数解,
∵x>0,
∴ax2+2x-1>0有正的实数解.
当a≥0时,显然满足;
当a<0时,只要△=4+4a>0,
∴-1<a<0,
综上所述,a>-1.
解法2:f′(x)=$\frac{1}{x}$-ax-2=$\frac{1-{ax}^{2}-2x}{x}$,
由题意可知f′(x)<0在(0,+∞)内有实数解.
即1-ax2-2x<0在(0,+∞)内有实数解.
即a>$\frac{1}{{x}^{2}}$-$\frac{2}{x}$在(0,+∞)内有实数解.
∵x∈(0,+∞)时,$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=($\frac{1}{x}$-1)2-1≥-1,
∴a>-1.
点评 本题考查了导数与函数的单调性之间的关系,可从方程的观点与函数的观点解答,属于中档题.

 计算高手系列答案
计算高手系列答案| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | -$\frac{2\sqrt{6}}{5}$ |
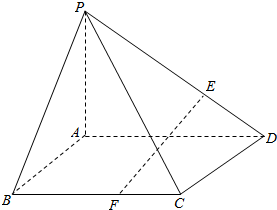 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC