题目内容
10．直线y=-x+m与曲线（y-$\sqrt{9-{x}^{2}}$）（x+$\sqrt{9-{y}^{2}}$）=0恰有一个公共点，求实数m的取值范围．分析 确定曲线（y-$\sqrt{9-{x}^{2}}$）（x+$\sqrt{9-{y}^{2}}$）=0表示圆x2+y2=9在第二象限的部分，包括与坐标轴的交点，
解答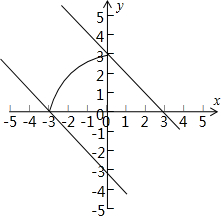 
解：曲线（y-$\sqrt{9-{x}^{2}}$）（x+$\sqrt{9-{y}^{2}}$）=0表示圆x2+y2=9在第二象限的部分，包括与坐标轴的交点，
因为直线y=-x+m与曲线（y-$\sqrt{9-{x}^{2}}$）（x+$\sqrt{9-{y}^{2}}$）=0恰有一个公共点，
所以直线经过（0，3），（-3，0）时，m取得最大与最小，
所以-3≤m≤3．
点评 本题考查直线与圆的位置关系，考查学生分析解决问题的能力，比较基础．
练习册系列答案
名师点拨卷系列答案
相关题目
1．已知函数f（x）=log2x，若在[1，8]上任取一个实数x0，则不等式1≤f（x0）≤2成立的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{7}$ | D． | $\frac{1}{2}$ |
如图，有一景区的平面图是一半圆形，其中AB长为2km，C、D两点在半圆弧上，满足BC=CD，设∠COB=θ．
15．复数z满足z（3-4i）=1（i是虚数单位），则|z|=（ ）
| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{5}}}{25}$ | C． | $\frac{1}{25}$ | D． | $\frac{1}{5}$ |