题目内容
(本小题满分14分)
已知棱长为1的正方体ABCD-A1B1C1D1中,P在对角线A1C1上,记二面角P-AB-C为α,二面角P-BC-A为β。
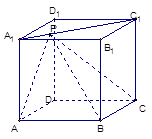
(1)当A1P:PC1=1:3时,求cos(α+β)的大小。
(2)点P是线段A1C1(包括端点)上的一个动点,问:当点P在什么位置时,α+β有最小值?
已知棱长为1的正方体ABCD-A1B1C1D1中,P在对角线A1C1上,记二面角P-AB-C为α,二面角P-BC-A为β。

(1)当A1P:PC1=1:3时,求cos(α+β)的大小。
(2)点P是线段A1C1(包括端点)上的一个动点,问:当点P在什么位置时,α+β有最小值?
(1)- (2)P为A1C1的中点
(2)P为A1C1的中点
 (2)P为A1C1的中点
(2)P为A1C1的中点试题分析:
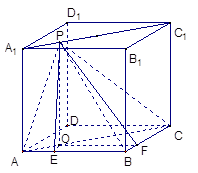
作PO⊥面ABCD于O,作OE⊥AB于E,OF⊥BC于F
∵正方体ABCD-A1B1C1D1
∴点O在线段AC上,且AO:OC=1:3
∴α=∠PEO,β=∠PFO
EO=
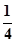 ,FO=
,FO=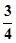 ,PO=1,PE=
,PO=1,PE=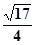 ,PF=
,PF=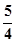 2分
2分cosα=
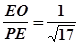 ,sinα=
,sinα=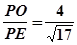 ,cosβ=
,cosβ=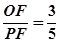 , sinβ=
, sinβ=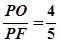
cos(α+β)=cosαcosβ-sinαsinβ=
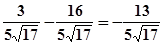 =-
=-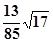 4分
4分(2)(8分)
设A1P=kA1C1,k∈[0,1] 5分
由第(1)题可知α=∠PEO,β=∠PFO
EO=k,FO=1-k,PO=1,PE=
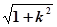 ,PF=
,PF=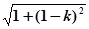
cosα=
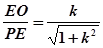 ,sinα=
,sinα=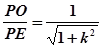 ,cosβ=
,cosβ=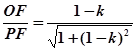 ,
, sinβ=
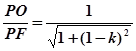 7分
7分当k=0或1时,即点P与A1或C1重合时,其中一个角为
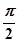 ,另一个角为
,另一个角为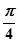 ,
,此时α+β=
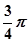 ,tan(α+β)= -1 8分
,tan(α+β)= -1 8分∴当k≠0,且k≠1时,tanα=
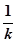 ,tanβ=
,tanβ=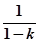
∴tan(α+β)
=
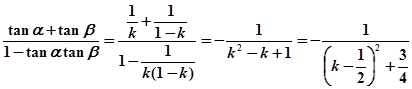 11分
11分∵k∈(0,1) ∴
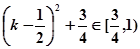 ∴tan(α+β)∈
∴tan(α+β)∈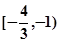
∵
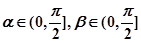 ∴
∴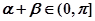
∴tan(α+β)=
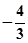 时,α+β有最小值,此时k=
时,α+β有最小值,此时k=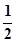 时,即点P为A1C1的中点。 14分
时,即点P为A1C1的中点。 14分点评:本题有一定难度,多章节知识的综合

练习册系列答案
相关题目

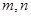 是不同的直线,
是不同的直线,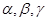 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: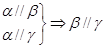 ②
②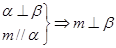 ③
③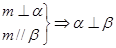 ④
④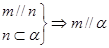
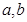 和平面
和平面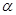 ,且
,且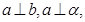 则
则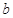 与
与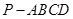 的底面
的底面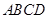 为矩形,且
为矩形,且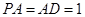 ,
,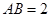 ,
,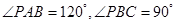 ,(Ⅰ)平面
,(Ⅰ)平面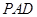 与平面
与平面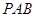 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线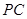 与平面
与平面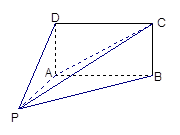
 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
,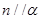 ,则
,则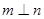 ②若
②若 ,
,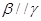 ,
,
 ,
,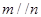 ④若
④若 ,
, ,则
,则
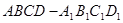 中,二面角
中,二面角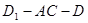 的正切值为
的正切值为
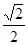
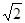 .
.