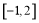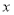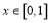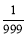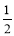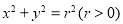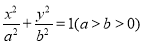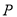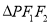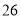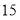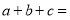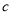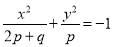题目内容
以椭圆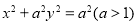 的一个顶点
的一个顶点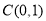 为直角顶点作此椭圆的内接等腰直角三角形
为直角顶点作此椭圆的内接等腰直角三角形 ,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
(1)存在,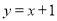 与
与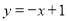 ;(2)存在,最多有
;(2)存在,最多有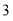 个.
个.
【解析】
试题分析:(1)这样的等腰直角三角形存在.直线y=x+1与直线y=-x+1满足题意;
(2)设出CA所在的直线方程,代入椭圆的方程并整理,求出|CA|,同理求出|CB|,由|CA|=|CB|得(k-1)[k2-(a2-1)k+1]=0,讨论方程根的情况,即可得出结论.
试题解析:(1)这样的等腰直角三角形存在。因为直线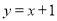 与直线
与直线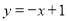 垂直,且关于
垂直,且关于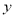 轴对称,所以直线
轴对称,所以直线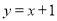 与直线
与直线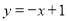 是一个等腰直角三角形两腰所在的直线方程。
是一个等腰直角三角形两腰所在的直线方程。
(2)设 两点分别居于
两点分别居于 轴的左,右两侧,设
轴的左,右两侧,设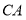 的斜率为
的斜率为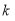 ,则
,则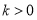 ,
,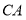 所在的直线方程为
所在的直线方程为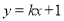 ,代入椭圆的方程并整理得
,代入椭圆的方程并整理得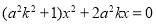 ,
,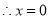 或
或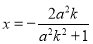 ,
,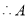 的横坐标为
的横坐标为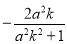 ,
,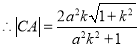 ,
,
同理可得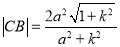 ,所以由
,所以由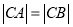 得
得
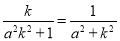 ,
,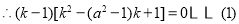 ,
,
当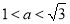 时,(1)的解是
时,(1)的解是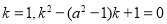 无实数解;
无实数解;
当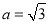 时,(1)的解是
时,(1)的解是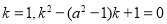 的解也是
的解也是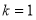 ;当
;当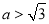 时,(1)的解除
时,(1)的解除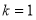 外,方程
外,方程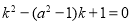 有两个不相等的正根,且都不等于,故(1)有
有两个不相等的正根,且都不等于,故(1)有 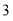 个正根。
个正根。
所以符合题意的等腰直角三角形一定存在,最多有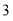 个。
个。
考点:(1)椭圆的性质;(2)直线与圆锥曲线的应用.

练习册系列答案
相关题目