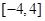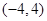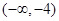题目内容
函数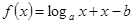 (2〈a〈3〈b〈4)的零点所在的一个区间是
(2〈a〈3〈b〈4)的零点所在的一个区间是
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
C
解析试题分析:因为f(1)=1-b<0,f(2)=  <0,f(3) =
<0,f(3) =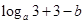 >0,所以函数
>0,所以函数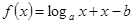 (2〈a〈3〈b〈4)的零点所在的一个区间是(2,3),选C。
(2〈a〈3〈b〈4)的零点所在的一个区间是(2,3),选C。
考点:本题主要考查函数零点存在定理。
点评:简单题,函数在区间(a,b)有零点,f(a)f(b)<0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知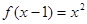 ,则
,则 的表达式为 ( )
的表达式为 ( )
A. | B. |
C.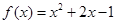 | D. |
已知函数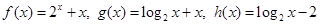 的零点依次为
的零点依次为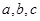 ,则( )
,则( )
A.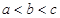 | B.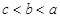 | C.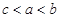 | D.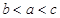 |
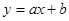 与
与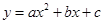 的图象关系可能正确的是( )
的图象关系可能正确的是( )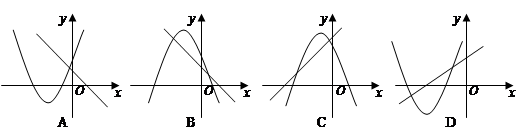
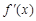 的图象如右图所示,那么函数f (x)的图象最有可能的是
的图象如右图所示,那么函数f (x)的图象最有可能的是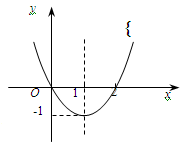
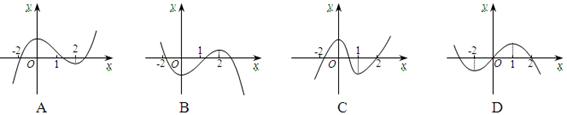
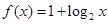 与
与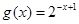 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )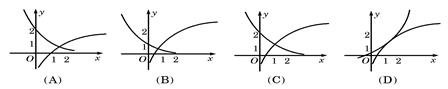
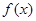 在定义域内可导,
在定义域内可导,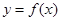 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数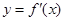 的图象可能是
的图象可能是
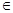 R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )
R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )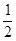
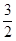
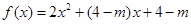 ,
,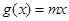 ,若对于任一实数
,若对于任一实数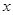 ,
,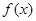 与
与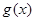 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数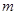 的取值范围是( )
的取值范围是( )