Question

【题目】已知数列的前项和为，且满足：，，

(1)、求数列的前项和为；

（2）、若不等式恒成立，求实数的取值范围。

Answer 1

【答案】(1)

【解析】

由题知，当n≥2 时，有Sn+1=an+2﹣an+1，Sn﹣1+1=an+1﹣an，两式相减得an+2=2an+1，利用等

比数列的通项公式与求和公式可得an，Sn.(2)由题得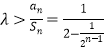再利用数列的单调性即可得出实数的取值范围．

由题知，当n≥2 时，有Sn+1=an+2﹣an+1，Sn﹣1+1=an+1﹣an，

两式相减得an+2=2an+1，

又a1=1，a2=2， a3=4，故an+1=2an 对任意n∈N* 成立，

∴，

（2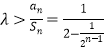）恒成立，只需的最大值，

当n=1时，右式取得最大值1，∴λ＞1．

故答案为：λ＞1．