题目内容
5.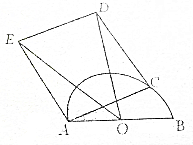 如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.
如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.(1)试将S表示成关于α的函数;
(2)求S的最大值,并求S取得最大值时α的大小.
分析 (1)如图所示,作OG⊥DE于G,S=12DE×OG12DE×OG,求出DE,OG,即可将S表示成关于α的函数;
(2)利用辅助角公式化简函数,即可求S的最大值,并求S取得最大值时α的大小.
解答 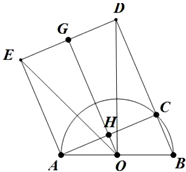 解:(1)如图所示,作OG⊥DE于G,
解:(1)如图所示,作OG⊥DE于G,
∵AB为直径,
∴∠ACB=90°,
∵A,C,D,E为正方形,
∴∠ACD=90°,
∴B,C,D在同一直线上,OG∥BD,
∵AE=DE=DC=AC=ABcosα=2cosα,BC=ABsinα=2sinα,
∴BD=DC+BC=2(cosα+sinα),
∵OG是梯形ABDE的中位线,
∴OG=12(AE+BD)=2cosα+sinα,
∴S=12DE×OG=12×2cosα×(2cosα+sinα)=cos2α+sin2α+1;
(2)S=cos2α+sin2α+1=√2sin(2α+π4)+1,
∴2α+π4=π2,即α=π8时,S取最大值√2-1.
点评 本题考查三角形面积的计算,考查辅助角公式,正确表示三角形的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目