题目内容
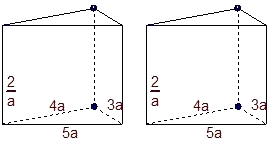
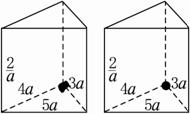
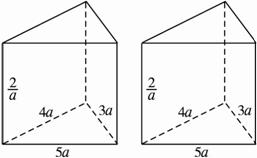
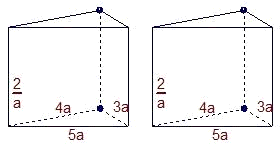有两个相同的直三棱柱，高为
，底面三角形的三边长分别为3a，4a，5a（a＞0），用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a的取值范围是________．
0＜a＜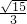
分析：由题意拼成一个三棱柱，求出表面积，拼成一个四棱柱，3种情况分别求出表面积，然后确定a的值．
解答：①拼成一个三棱柱时，只有一种一种情况，就是将上下底面对接，其全面积为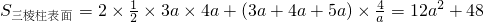
．
②拼成一个四棱柱，有三种情况，就是分别让边长为3a，4a，5a所在的侧面重合，其上下底面积之和都是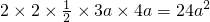
，但侧面积分别为：
，
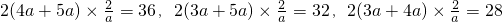显然，三个是四棱柱中全面积最小的值为：
．
由题意，得24a2+28＜12a2+48，
解得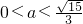
．
故答案为：0＜a＜
点评：本题考查棱柱、棱锥、棱台的侧面积和表面积，考查空间想象能力，计算能力，是基础题．
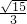
分析：由题意拼成一个三棱柱，求出表面积，拼成一个四棱柱，3种情况分别求出表面积，然后确定a的值．
解答：①拼成一个三棱柱时，只有一种一种情况，就是将上下底面对接，其全面积为
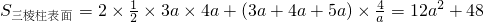．②拼成一个四棱柱，有三种情况，就是分别让边长为3a，4a，5a所在的侧面重合，其上下底面积之和都是
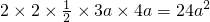，但侧面积分别为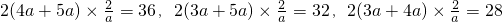：，显然，三个是四棱柱中全面积最小的值为：
．由题意，得24a2+28＜12a2+48，
解得
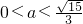．故答案为：0＜a＜
点评：本题考查棱柱、棱锥、棱台的侧面积和表面积，考查空间想象能力，计算能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
，底面三角形的三边长分别为
，底面三角形的三边长分别为3a,4a,5a(a＞0).用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的是一个四棱柱，则a的取值范围是_________.
，底面三角形的三边长分别为3a,4a,5a(a＞0).用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a的取值范围是 .
，底面三角形的三边长分别为3a、4a、5a(a＞0),用它们拼成一个三棱柱或四棱柱，在所有的情形中，全面积最小的是一个四棱柱，则a的取值范围是__________.