题目内容
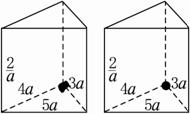
有两个相同的直三棱柱,高为| 2 | a |
分析:由题意拼成一个三棱柱,求出表面积,拼成一个四棱柱,3种情况分别求出表面积,然后确定a的值.
解答:解:①拼成一个三棱柱时,有三种情况,将上下底面对接,其全面积为S三棱柱表面=2×
×3a×4a+(3a+4a+5a)×
=12a2+48.
3a边可以合在一起时,S三棱柱表面=2×2×
×3a×4a+2(5a+4a)×
=24a2+36
4a边合在一起时S三棱柱表面=2×2×
×3a×4a+2(5a+3a)×
=24a2+32.
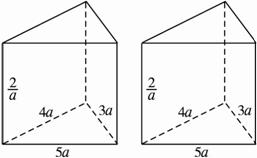
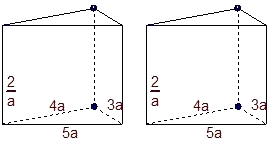
②拼成一个四棱柱,有三种情况,就是分别让边长为3a,4a,5a所在的侧面重合,其上下底面积之和都是2×2×
×3a×4a=24a2,但侧面积分别为:2(4a+5a)×
=36,2(3a+5a)×
=32,2(3a+4a)×
=28,
显然,三个是四棱柱中全面积最小的值为:S四棱柱表面=2×2×
×3a×4a+2(3a+4a)×
=24a2+28.
由题意,得24a2+28<12a2+48,
解得0<a<
.
故答案为:0<a<
| 1 |
| 2 |
| 4 |
| a |
3a边可以合在一起时,S三棱柱表面=2×2×
| 1 |
| 2 |
| 2 |
| a |
4a边合在一起时S三棱柱表面=2×2×
| 1 |
| 2 |
| 2 |
| a |
②拼成一个四棱柱,有三种情况,就是分别让边长为3a,4a,5a所在的侧面重合,其上下底面积之和都是2×2×
| 1 |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
显然,三个是四棱柱中全面积最小的值为:S四棱柱表面=2×2×
| 1 |
| 2 |
| 2 |
| a |
由题意,得24a2+28<12a2+48,
解得0<a<
| ||
| 3 |
故答案为:0<a<
| ||
| 3 |
点评:本题考查棱柱、棱锥、棱台的侧面积和表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目