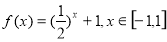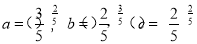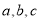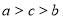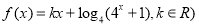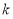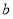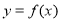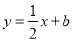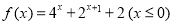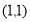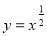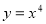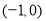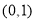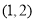题目内容
设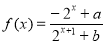 (
(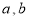 为实常数).
为实常数).
(1)当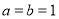 时,证明:
时,证明:
①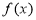 不是奇函数;②
不是奇函数;②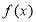 是
是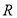 上的单调递减函数.
上的单调递减函数.
(2)设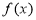 是奇函数,求
是奇函数,求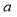 与
与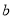 的值.
的值.
(1)见解析;(2) 或
或 .
.
【解析】
试题分析:(1)①利用特殊值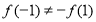 可证
可证 不是奇函数;②利用单调性的定义进行证明函数的单调性,经五步:取值,作差,化简,判断符号,下结论.(2)方法一:由
不是奇函数;②利用单调性的定义进行证明函数的单调性,经五步:取值,作差,化简,判断符号,下结论.(2)方法一:由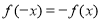 代入化简得:
代入化简得:
 ,这是关于
,这是关于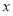 的恒等式,所以
的恒等式,所以 ;方法二:由
;方法二:由 算出
算出 与
与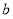 的值,然后进行检验,考虑到分母不能为0,注意分
的值,然后进行检验,考虑到分母不能为0,注意分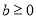 与
与 两种情况进行讨论.
两种情况进行讨论.
试题解析:(1)①当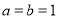 时,
时, ,
,
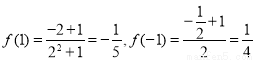 ,
,
所以 ,
,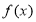 不是奇函数; 2分
不是奇函数; 2分
②设 ,则
,则 , 3分
, 3分

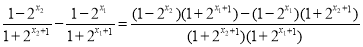
 5分
5分
因为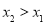 ,所以
,所以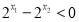 ,又因为
,又因为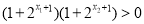 ,
,
所以 6分
6分
所以 ,
,
所以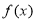 是
是 上的单调递减函数. 7分
上的单调递减函数. 7分
(2)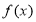 是奇函数时,
是奇函数时, ,
,
即 对任意实数
对任意实数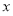 成立,
成立,
化简整理得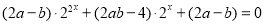 ,这是关于
,这是关于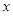 的恒等式, 10分
的恒等式, 10分
所以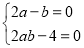 所以
所以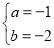 或
或 . 12分
. 12分
(2)另【解析】
若 ,则由
,则由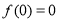 ,得
,得 ; 8分
; 8分
由 ,解得:
,解得: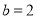 ; 9分
; 9分
经检验符合题意. 10分
若 ,则由
,则由 ,得
,得 ,
,
因为奇函数的定义域关于原点对称,
所以 ,所以
,所以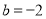 , 11分
, 11分
由 ,解得:
,解得: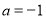 ;
;
经检验符合题意。
所以 . 12分
. 12分
考点:函数的奇偶性,单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目