题目内容
如图所示,有两条相交成 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 点
点 km,乙离
km,乙离 点
点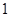 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行.
⑴起初,两人的距离是多少?
⑵用包含 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
⑶什么时候两人的距离最短?
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 点
点 km,乙离
km,乙离 点
点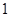 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行.⑴起初,两人的距离是多少?
⑵用包含
 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;⑶什么时候两人的距离最短?

(1)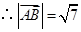 km.(2)当
km.(2)当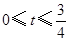 时,
时,
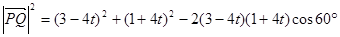 ------------6分
------------6分
当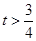 时,
时,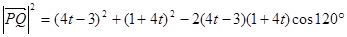
(3)当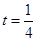 小时时,即在第
小时时,即在第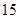 分钟末,
分钟末,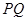 最短,最短距离是
最短,最短距离是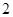 km
km
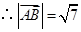 km.(2)当
km.(2)当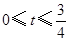 时,
时,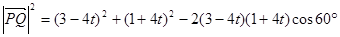 ------------6分
------------6分当
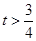 时,
时,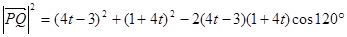
(3)当
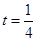 小时时,即在第
小时时,即在第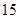 分钟末,
分钟末,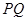 最短,最短距离是
最短,最短距离是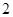 km
km(1)解题的关键是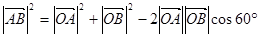 .
.
(2)设甲、乙两人 小时后的位置分别是
小时后的位置分别是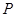 ,
,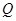 ,则
,则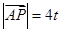 ,
,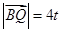 ,
,
然后要对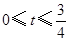 和
和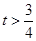 两种情况讨论.
两种情况讨论.
(3) 本题实质是求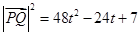 的最小值.
的最小值.
解:⑴设甲、乙两人最初的位置是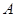 ,
,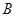 ,
,
则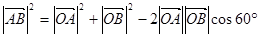
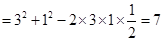 ,
,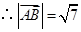 km.----------------4分
km.----------------4分
⑵设甲、乙两人 小时后的位置分别是
小时后的位置分别是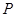 ,
,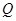 ,
,
则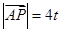 ,
,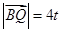 .
.
当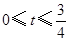 时,
时,
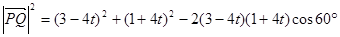 ------------6分
------------6分
当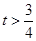 时,
时,
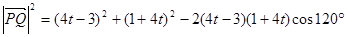 .---------------8分
.---------------8分
⑶上面两式实际上是统一的,所以
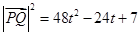 ,------------------10分
,------------------10分
即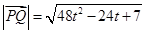 .
.
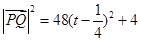 ,
,
 当
当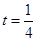 小时时,即在第
小时时,即在第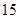 分钟末,
分钟末,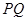 最短,最短距离是
最短,最短距离是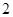 km.
km.
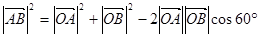 .
.(2)设甲、乙两人
 小时后的位置分别是
小时后的位置分别是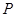 ,
,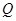 ,则
,则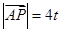 ,
,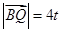 ,
,然后要对
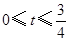 和
和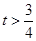 两种情况讨论.
两种情况讨论.(3) 本题实质是求
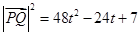 的最小值.
的最小值.解:⑴设甲、乙两人最初的位置是
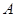 ,
,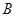 ,
,则
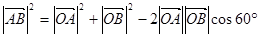
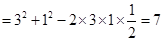 ,
,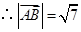 km.----------------4分
km.----------------4分⑵设甲、乙两人
 小时后的位置分别是
小时后的位置分别是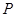 ,
,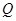 ,
,则
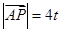 ,
,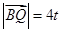 .
.当
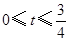 时,
时,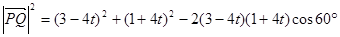 ------------6分
------------6分当
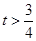 时,
时,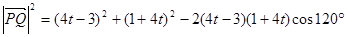 .---------------8分
.---------------8分⑶上面两式实际上是统一的,所以
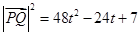 ,------------------10分
,------------------10分即
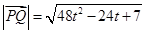 .
.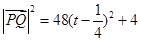 ,
, 当
当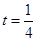 小时时,即在第
小时时,即在第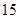 分钟末,
分钟末,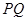 最短,最短距离是
最短,最短距离是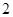 km.
km.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 =Asin(ωx+ф)(A>0,ω>0)的图像在y轴右侧的第一个最高点为M(2,2),与x轴在原点右侧的第一个交点为N(5,0),则函数
=Asin(ωx+ф)(A>0,ω>0)的图像在y轴右侧的第一个最高点为M(2,2),与x轴在原点右侧的第一个交点为N(5,0),则函数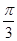 x+
x+ )
) 是函数
是函数 的一个对称中心;②若
的一个对称中心;②若 是第一象限角,且
是第一象限角,且 ,则
,则 ;③函数
;③函数 是偶函数;④定义平面向量之间的一种新运算“
是偶函数;④定义平面向量之间的一种新运算“ ”如下:对任意的
”如下:对任意的 ,
, ,若
,若

 ,则
,则
 .
. 
 时,求函数f(x) 的最大值和最小值
时,求函数f(x) 的最大值和最小值 (
( )的图象
)的图象 的解析式是( )
的解析式是( ) 




 =(cos
=(cos +sin
+sin =(cos
=(cos ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.  在区间
在区间 上的最大值为__ __
上的最大值为__ __ 中,角
中,角 所对边分别是
所对边分别是 ,若
,若 ,则
,则 .
. 的图象向右平移
的图象向右平移 个单位得到的函数解析式为
个单位得到的函数解析式为