题目内容
已知函数 (
( 为常数)在
为常数)在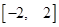 上有最大值3,那么此函数在
上有最大值3,那么此函数在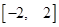 上的最小值为( )
上的最小值为( )
| A.-29 | B.-37 | C.-5 | D.-1 |
B
解析试题分析:因为 ,所以
,所以 ,由
,由 =0得,X=0,或x=2,计算f(-2)=m-40,f(0) ="m,f(2)" =m-8,所以m=3,故最小值为m-40=-37,选B。
=0得,X=0,或x=2,计算f(-2)=m-40,f(0) ="m,f(2)" =m-8,所以m=3,故最小值为m-40=-37,选B。
考点:本题主要考查导数计算,函数最值的概念及求法。
点评:典型题,利用导数求函数的最值,是高考常见题目。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值及端点函数值、比较确定最大值最小值。

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
设函数 ,则该函数曲线在
,则该函数曲线在 处的切线与曲线
处的切线与曲线 围成的封闭图形的面积是 ( )
围成的封闭图形的面积是 ( )
A. | B. | C. | D. |
函数 在闭区间[-3,0]上的最大值、最小值分别是( )
在闭区间[-3,0]上的最大值、最小值分别是( )
| A.1,-1 | B. 3,-17 | C. 1,-17 | D.9,-19 |
已知函数 ,则
,则 ( )
( )
| A.-1 | B.-3 | C.2 | D.-2 |
曲线 在点P(1,12)处的切线与两坐标轴围成三角形的面积是
在点P(1,12)处的切线与两坐标轴围成三角形的面积是
| A.75 | B. | C.27 | D. |
设连续函数 ,则当
,则当 时,定积分
时,定积分 的符号( )
的符号( )
| A.一定是正的 |
| B.一定是负的 |
C.当 时是正的,当 时是正的,当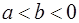 时是负的 时是负的 |
| D.以上结论都不对 |
由直线 ,曲线
,曲线 及
及 轴所围图形的面积为
轴所围图形的面积为
| A.3 | B.7 | C. | D. |
函数 在
在 处的切线方程是
处的切线方程是
A. | B. |
C. | D. |
 在定义域内可导,
在定义域内可导, 的图象如图所示,则导函数
的图象如图所示,则导函数 可能为
可能为
