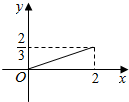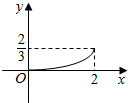题目内容
19.已知函数f(x)=$\frac{x}{1+|x|}$(x∈R) 时,则下列结论正确的是( )(1)?x∈R,等式f(-x)+f(x)=0恒成立
(2)?m∈(0,1),使得方程|f(x)|=m有两个不等实数根
(3)?x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2)
(4)?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点.
| A. | (1)(2) | B. | (2)(3) | C. | (1)(2)(3) | D. | (1)(3)(4) |
分析 画出函数f(x)=$\frac{x}{1+|x|}$的图象,分析函数f(x)=$\frac{x}{1+|x|}$的性质,逐一分析四个结论的正误,可得答案.
解答 解:∵函数f(x)=$\frac{x}{1+|x|}$的图象如下图所示:
对于(1),由图可得:函数图象关于原点对称,函数为奇函数,
∴?x∈R,等式f(-x)+f(x)=0恒成立,故(1)正确;
对于(2),?m∈(0,1),|f(x)|=m时,|f(-x)|=m,
∴方程|f(x)|=m均有两个不等实数根,故(2)正确;
对于(3),函数在定义R为增函数,
∴?x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2),故(3)正确;
对于(4),当k∈(1,+∞),使得函数f(x)的图象与y=k仅交于原点,
∴?k∈(1,+∞),函数g(x)=f(x)-kx在R上仅有一个零点.故(4)错误,
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了函数的单调性,奇偶性,零点,全称命题与特称命题等知识点,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.函数f(x)=log2x-(x-1)2+2的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.若x1满足3x-1=2-x,x2满足log3(x-1)+x-2=0,则x1+x2等于( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
7.抛物线x2=2py,(p>0)在x=1处的切线方程为2x-2y-1=0,则抛物线的准线为( )
| A. | x=-$\frac{1}{2}$ | B. | x=-1 | C. | y=-$\frac{1}{2}$ | D. | y=-1 |
11.定义在R上的偶函数f(x)的周期为2,0<x<1,f(x)=-log2(1-x),则当1<x<2,下面说法正确的是( )
| A. | f(x)单调递增,f(x)<0 | B. | f(x)单调递增,f(x)>0 | C. | f(x)单调递减,f(x)<0 | D. | f(x)单调递减,f(x)>0 |
 如图,过椭圆的左顶点A作两条互相垂直的直线分别交椭圆与P、Q连接PQ.
如图,过椭圆的左顶点A作两条互相垂直的直线分别交椭圆与P、Q连接PQ. 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F在线段A1B1上运动,且|EF|=1,点G在线段AD上运动,H是线段CD的中点,设DG=x(0<x<2),则三棱锥G-EFH的体积V(x)的图象大致是( )
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F在线段A1B1上运动,且|EF|=1,点G在线段AD上运动,H是线段CD的中点,设DG=x(0<x<2),则三棱锥G-EFH的体积V(x)的图象大致是( )