题目内容

9．函数f（x）=log2x-（x-1）2+2的零点个数为（　　）
A．0B．1C．2D．3

分析 问题转化为求函数的交点问题，画出函数的图象，数出交点个数即可．

解答 解：令f（x）=0，
得：log2x=（x-1）2-2，
画出函数y=log2x和y=（x-1）2-2的图象，
如图示：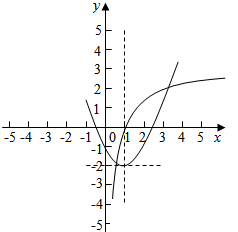
，
由图象得：函数有2个交点，即函数f（x）有2个零点，
故选：C．

点评 本题考查了函数的零点问题，考查数形结合思想，是一道基础题．

练习册系列答案
相关题目
19．已知角α终边经过点 P（-5，-12），则 tanα 的值是（　　）
A．$\frac{12}{5}$B．-$\frac{12}{5}$C．$\frac{5}{12}$D．-$\frac{5}{12}$
20．实数a＞1，b＞1是a+b＞2的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
17．已知不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+2y-4≤0}\end{array}\right.$表示的平面区域恰好被面积最小的圆C：（x-a）2+（y-b）2=r2及其内部所覆盖，则圆C的方程为（　　）
A．（x-1）2+（y-2）2=5B．（x-2）2+（y-1）2=8C．（x-4）2+（y-1）2=6D．（x-2）2+（y-1）2=5
4．已知sinθ，sinα，cosθ为等差数列，sinθ，sinβ，cosθ为等比数列，则cos2α-$\frac{1}{2}$cos2β=0．
14．已知数列{an}的前n项和${S_n}={n^2}$，则a5的值为（　　）
A．9B．11C．15D．25
1．一个三角形的三个内角A，B，C 成等差数列，那么tan（A+C）的值是$-\sqrt{3}$．
18．下列函数中，在区间（1，+∞）上为增函数的是（　　）
A．y=-3x+1B．y=$\frac{2}{x}$C．y=x2-4x+5D．y=|x-1|+2
19．已知函数f（x）=$\frac{x}{1+|x|}$（x∈R） 时，则下列结论正确的是（　　）
（1）?x∈R，等式f（-x）+f（x）=0恒成立
（2）?m∈（0，1），使得方程|f（x）|=m有两个不等实数根
（3）?x1，x2∈R，若x1≠x2，则一定有f（x1）≠f（x2）
（4）?k∈（1，+∞），使得函数g（x）=f（x）-kx在R上有三个零点．
A．（1）（2）B．（2）（3）C．（1）（2）（3）D．（1）（3）（4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网