题目内容
已知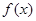 为偶函数,且
为偶函数,且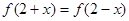 ,当
,当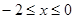 时,
时,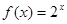 ,若
,若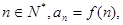 则
则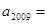 ( )
( )
A.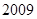 | B.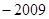 | C.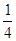 | D. |
C
解析考点:数列递推式;偶函数.
分析:由f(x)为偶函数,且f(2+x)=f(2-x),推出f(x)是周期为4的周期函数,由an=f(n)得,a2010=f(2009)=f(4×502+1)=f(1)=f(-1),于是即可求出a2009的值.
解:∵f(2+x)=f(2-x),∴f(x)="f" (4-x),又f(x)为偶函数,
∴f(-x)=f(x),
∴f(-x)=f(4-x),
∴f(x)=f(x+4),
∴f(x)是周期等于4的周期函数,
∵an="f" (n),当-2≤x≤0时,f(x)=2x,
∴a2009="f" (2009)="f" (4×502+1)="f" (1)=f(-1)=2-1= ,
,
故选C.

练习册系列答案
相关题目
已知f(x)为偶函数,且f (2+x)=f (2-x),当-2≤x≤0时,f(x)=2x,an=f (n),n∈N*,则a2010的值为( )
| A、2010 | ||
| B、4 | ||
C、
| ||
| D、-4 |
已知函数f(x)为偶函数,且f(x+1)=
,且当x∈(0,1)时,f(x)=2x-1,则f(log212)的值为( )
| 1 |
| f(x) |
A、
| ||
B、
| ||
| C、2 | ||
| D、11 |