题目内容
已知函数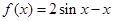 ,
, .
.
(1)讨论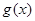 在
在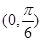 内和在
内和在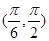 内的零点情况.
内的零点情况.
(2)设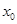 是
是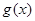 在
在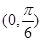 内的一个零点,求
内的一个零点,求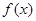 在
在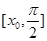 上的最值.
上的最值.
(3)证明对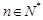 恒有
恒有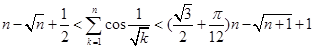 .
.
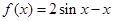 ,
, .
.(1)讨论
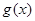 在
在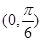 内和在
内和在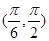 内的零点情况.
内的零点情况.(2)设
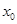 是
是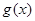 在
在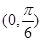 内的一个零点,求
内的一个零点,求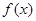 在
在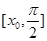 上的最值.
上的最值.(3)证明对
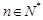 恒有
恒有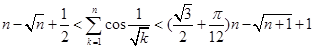 .
.(1) 在
在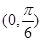 内有唯一零点;
内有唯一零点; 在
在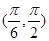 内无零点.(2)
内无零点.(2) 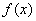 在
在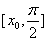 有最大值
有最大值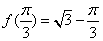 ;
;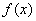 在
在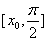 的最小值
的最小值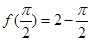 .(3)详见解析.
.(3)详见解析.
 在
在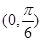 内有唯一零点;
内有唯一零点; 在
在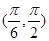 内无零点.(2)
内无零点.(2) 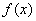 在
在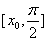 有最大值
有最大值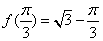 ;
;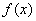 在
在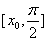 的最小值
的最小值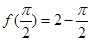 .(3)详见解析.
.(3)详见解析.试题分析:(1)首先求导确定
 在
在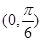 、
、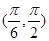 内的单调性,然后根据零点判定定理确定
内的单调性,然后根据零点判定定理确定 的零点情况; (2)求导得
的零点情况; (2)求导得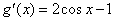 ,所以
,所以  在
在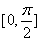 有最大值
有最大值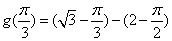 ,又
,又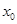 是
是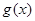 在
在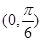 内的一个零点,所以
内的一个零点,所以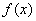 在
在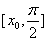 的最大值为
的最大值为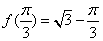 .再由(1)的结论知
.再由(1)的结论知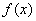 在
在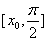 的最小值应为
的最小值应为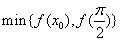 .由
.由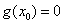 知
知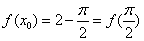 ,于是
,于是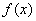 在
在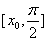 的最小值
的最小值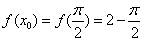 . (3)由(2)知
. (3)由(2)知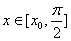 时,有
时,有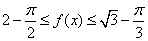 ,即
,即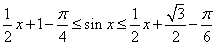 ,得
,得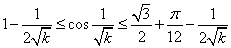 ,再将左右两边放缩相加即得.
,再将左右两边放缩相加即得.(1)
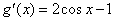 在
在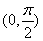 有唯一零点
有唯一零点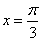 ,易知
,易知 在
在 单增而在
单增而在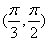
内单减,且
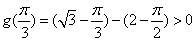 ,故
,故 在
在 和
和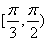 内都至多有一个零点.
内都至多有一个零点.又
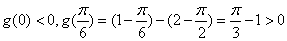 ,
,故
 在
在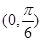 内有唯一零点;
内有唯一零点;再由
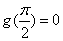 知
知 在
在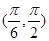 内无零点.
内无零点.(2)由(1)知
 在
在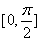 有最大值
有最大值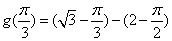 ,
,故
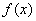 在
在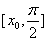 有最大值
有最大值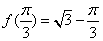 ;
;再由(1)的结论知
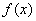 在
在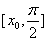 的最小值应为
的最小值应为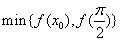 .
.由
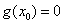 知
知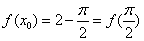 ,于是
,于是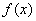 在
在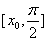 的最小值
的最小值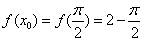 .
.(3)由(2)知
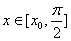 时,有
时,有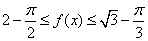 ,即
,即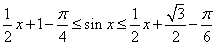 ①
①取
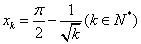 ,则
,则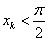 且
且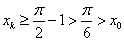 ,将
,将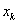 的值代入①中,可得
的值代入①中,可得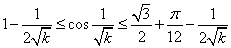
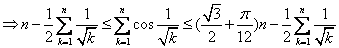 ②
②再由
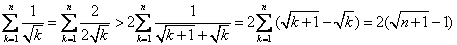 ,得
,得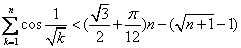 ③
③相仿地,
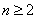 时,
时,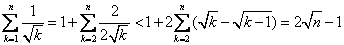 ,故
,故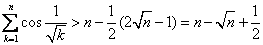 ④
④而
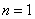 时④即
时④即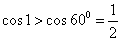 ,显然也成立.故原不等式成立.
,显然也成立.故原不等式成立.
练习册系列答案
相关题目
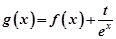 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;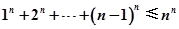 (n∈N*).
(n∈N*).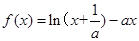 ,其中
,其中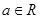 且
且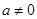 .
.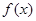 的单调性;
的单调性;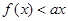 恒成立,求实数
恒成立,求实数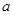 取值范围;
取值范围;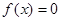 存在两个异号实根
存在两个异号实根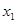 ,
,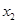 ,求证:
,求证: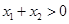
 在点(1,0)处的切线.
在点(1,0)处的切线.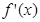 是函数
是函数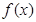 的导函数,将
的导函数,将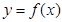 和
和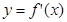 的图像画在同一个直角坐标系中,不可能正确的是( )
的图像画在同一个直角坐标系中,不可能正确的是( )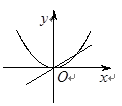
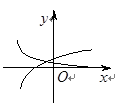
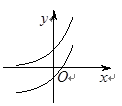
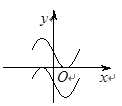
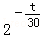 ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )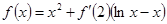 ,则
,则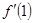 = ( )
= ( )