题目内容
设一直角三角形两直角边的长均是区间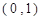 的随机数,则斜边的长小于
的随机数,则斜边的长小于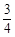 的概率为 。
的概率为 。

解析试题分析:由题意知本题是一个几何概型,是常说的“约会”问题,解法同一般的几何概型一样,看出试验包含的所有事件对应的集合,求出面积,写出满足条件的集合和面积,求比值即可。解:由题意知本题是一个几何概型,∵两直角边都是0,1间的随机数,设两直角边分别是x,y.∴试验包含的所有事件是{x,y|0<x<1,0<y<1},对应的正方形的面积是1,满足条件的事件对应的集合{(x,y)|x2+y2<9/16,x>0,y>0.},这个图形是一个1/4圆,面积是 ,题目即求它与边长为1的正方行面积的比P=
,题目即求它与边长为1的正方行面积的比P= ,故答案为
,故答案为
考点:几何概型
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
 由直线
由直线 和
和 所围成的平面图形,区域
所围成的平面图形,区域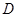 是由余弦函数
是由余弦函数 、
、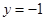 所围成的平面图形.在区域
所围成的平面图形.在区域 经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是 ;
经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是 ;
 ,
, 和
和 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以 表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号).
表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号). ;
;  ;
;  的值不能确定,因为它与
的值不能确定,因为它与
 与81
与81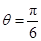 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是________.
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是________.