题目内容
【题目】设![]() 定义
定义![]() 且
且![]() 为常数),若
为常数),若![]() ,
,![]() .下述四个命题:
.下述四个命题:
①![]() 不存在极值;
不存在极值;
②若函数![]() 与函数
与函数![]() 的图象有两个交点,则
的图象有两个交点,则![]() ;
;
③若![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若![]() ,则在
,则在![]() 的图象上存在两点,使得在这两点处的切线互相垂直
的图象上存在两点,使得在这两点处的切线互相垂直
A. ①③④B. ②③④C. ②③D. ②④
【答案】C
【解析】
对命题①:直接求![]() 的导数,采用零点存在定理判断是否存在极值即可
的导数,采用零点存在定理判断是否存在极值即可
对②若函数![]() 与函数
与函数![]() 的图象有两个交点,则函数
的图象有两个交点,则函数![]() 一定与
一定与![]() 相切,通过联立方程求解即可
相切,通过联立方程求解即可
对③④,需要先求出![]() 的导函数,根据导函数特点去判断两命题是否成立
的导函数,根据导函数特点去判断两命题是否成立
对命题①:![]() ,
,![]() ,即
,即![]() ,使得
,使得![]() ,
,![]()
![]() 存在极值,命题①错
存在极值,命题①错
对命题②,画出![]() 与函数
与函数![]() 的图像,如图所示:
的图像,如图所示:
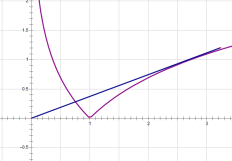
设切点横坐标为![]() ,此时
,此时![]() ,命题②正确
,命题②正确
对于命题③:![]()
![]() ,则
,则![]() ,
,
若![]() 在
在![]() 上是减函数,则
上是减函数,则![]() 对于
对于![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立, ![]() ,
,
![]() 恒成立,
恒成立,
![]() ,
,
![]() ;
;
即实数a的取值范围是![]() ,故③正确
,故③正确
对命题④:当![]() 时,
时,![]() ,
,
设![]()
![]() 是
是![]() 曲线上的任意两点,
曲线上的任意两点,
![]()
![]() ,
,
![]() ,
,
![]() 不成立.
不成立.
![]() 的曲线上不存的两点,使得过这两点的切线点互相垂直。命题④错误
的曲线上不存的两点,使得过这两点的切线点互相垂直。命题④错误
正确命题为②③,答案选C

练习册系列答案
相关题目