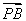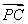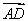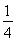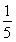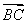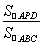题目内容
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l:x=2.
(1)求椭圆的标准方程;
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
(1)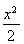 +y2=1.(2)ON=
+y2=1.(2)ON=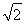 为定值
为定值
【解析】(1)∵椭圆C的短轴长为2,椭圆C的一条准线为l:x=2,
∴不妨设椭圆C的方程为 +y2=1.
+y2=1.
∴ =
=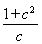 =2,即c=1.
=2,即c=1.
∴椭圆C的方程为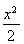 +y2=1.
+y2=1.
(2)F(1,0),右准线为l:x=2,设N(x0,y0),
则直线FN的斜率为kFN= ,直线ON的斜率为kON=
,直线ON的斜率为kON= ,
,
∵FN⊥OM,
∴直线OM的斜率为kOM=-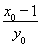 ,
,
∴直线OM的方程为:y=-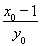 x,点M的坐标为M
x,点M的坐标为M  .
.
∴直线MN的斜率为kMN= .
.
∵MN⊥ON,∴kMN·kON=-1,
∴ ·
· =-1,
=-1,
∴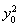 +2(x0-1)+x0(x0-2)=0,
+2(x0-1)+x0(x0-2)=0,
即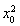 +
+ =2.∴ON=
=2.∴ON=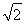 为定值
为定值

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目