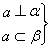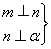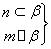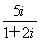题目内容
已知曲线C的极坐标方程是ρ＝2sin θ，直线l的参数方程是
(t为参数)．
(1)将曲线C的极坐标方程化为直角坐标方程；
(2)设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
(1) x2＋y2－2y＝0. (2)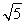
＋1
【解析】(1)曲线C的极坐标方程可化为ρ2＝2ρsin θ.
又x2＋y2＝ρ2，x＝ρcos θ，y＝ρsin θ，所以曲线C的直角坐标方程为x2＋y2－2y＝0.
(2)将直线l的参数方程化为直角坐标方程，
得y＝－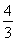
(x－2)．
令y＝0，得x＝2，即M点的坐标为(2,0)．
又曲线C为圆，圆C的圆心坐标为(0,1)，
半径r＝1，则MC＝
，
所以MN≤MC＋r＝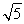
＋1，即MN的最大值为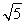＋1.
练习册系列答案
相关题目
