题目内容
(本小题满分12分)
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 个数据按照区间
个数据按照区间 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图
(1)若已知 位居民中月均用水量小于1吨的人数是12,求
位居民中月均用水量小于1吨的人数是12,求 位居民中月均用水量分别在区间
位居民中月均用水量分别在区间 和
和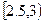 内的人数;
内的人数;
(2)在该市居民中随意抽取10位,求至少有2位居民月均用水量在区间 或
或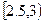 内的概率.(精确到0.01.参考数据:
内的概率.(精确到0.01.参考数据: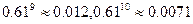 )
)
解:(1)根据频率直方图可得 位居民中月均用水量小于1吨的频率为
位居民中月均用水量小于1吨的频率为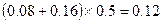 ……2分
……2分
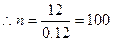 (人)……3分
(人)……3分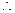 根据频率直方图可得
根据频率直方图可得 位居民中月均
位居民中月均
用水量在区间 内的人数是
内的人数是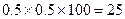 (人)……5分
(人)……5分
在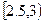 内的人数是
内的人数是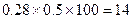 (人)……7分
(人)……7分
(2)设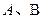 分别表示随机事件“居
分别表示随机事件“居
民月均用水量在区间 内”和
内”和
“居民月均用水量在区间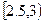 内”,
内”,
则事件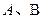 互斥. ……8分
互斥. ……8分 居民月均用水量在区间
居民月均用水量在区间 或
或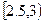 内的概率是
内的概率是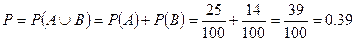 ……9分
……9分
设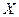 表示10位居民中月均用水量在区间
表示10位居民中月均用水量在区间 或
或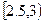 内的人数,则
内的人数,则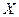 ~
~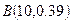 ……10分
……10分 所求概率是
所求概率是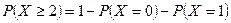
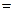
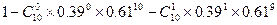
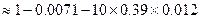
 ……12分
……12分
解析

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
10分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |  |  |  | 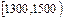 |  | 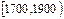 |  |
| 组数 | 48 | 121 | 208 | 223 | 193 | 165 | 42 |
| 频率 | | | | | | | |
(2) 根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3) 该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率
(本小题满分12分)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 |  合计 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是
 多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
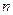 件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把
件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把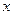 件打成一包,对这
件打成一包,对这 果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了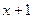 次
次 测这
测这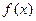 ;
;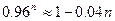 ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品?
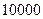 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组 之间).
之间).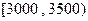 之间的人数;
之间的人数;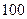 人作进一步分析,则月收入在
人作进一步分析,则月收入在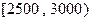 的这段应抽多少人?
的这段应抽多少人?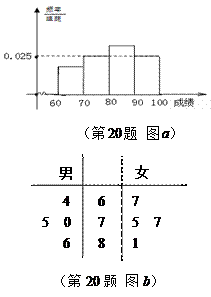
 学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.
学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.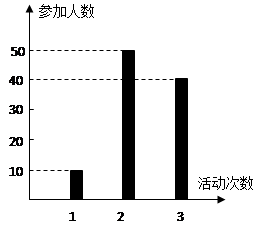
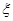 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量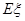 .
.