题目内容
.(本题满分12分)
 |
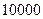 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在
 之间).
之间).(Ⅰ)根据频率分布直方图估计样本
数据的中位数所在的区间;
(Ⅱ)求被调查居民月收入在
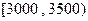 之间的人数;
之间的人数;(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这
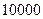 人中,用分层抽样方法抽出
人中,用分层抽样方法抽出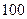 人作进一步分析,则月收入在
人作进一步分析,则月收入在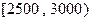 的这段应抽多少人?
的这段应抽多少人?
解:(Ⅰ)由于前两个矩形的面积和小于0.5,而前三个矩形的面积和大于0.5,所以中位数在第三个区间内,即中位数在[2000,2500). …………4分
(Ⅱ)月收入在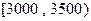 的频率为
的频率为 .
.
所以,月收入在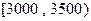 的人数为10000×0.15=1500. …………8分
的人数为10000×0.15=1500. …………8分
(Ⅲ)居民月收入在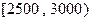 的频率为
的频率为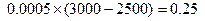 ,
,
所以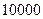 人中月收入在
人中月收入在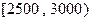 的人数为
的人数为 (人),
(人),
再从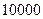 人用分层抽样方法抽出
人用分层抽样方法抽出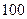 人,则月收入在
人,则月收入在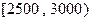 的这段应抽取
的这段应抽取 人. …………12分
人. …………12分
解析

练习册系列答案
相关题目
(本题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?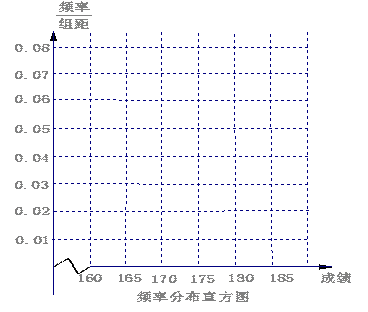
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 |  | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 |  | 20 | 0.200 |
| 第5组 | 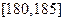 | 10 | 0.100 |
| 合计 | 100 | 1.000 | |
|
某高级中学共有学生2000名,各年级男、女生人数如下表:
| | 高一年级 | 高二年级 | 高三年级 |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
(Ⅰ)求x的值;
(Ⅱ)现
 用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名? (本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
 | 14 | 16 | 18 | 20 | 22 |
 | 12 | 10 | 7 | 5 | 3 |
 关于
关于 的散点图
的散点图(2)用最小二乘法求出回归直线方程
(3)计算
 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。 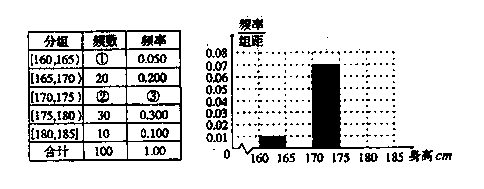
 ,求
,求 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图 和
和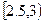 内的人数;
内的人数;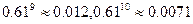 )
)
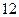 分)
分)
 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的 绝对值不超过
绝对值不超过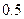 的概率.
的概率.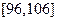 (单位:厘米),样本数据分组为
(单位:厘米),样本数据分组为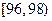 ,
,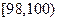 ,
,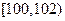 ,
,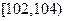 ,
, ,
,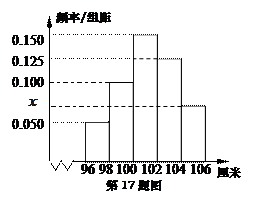
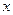 的值;
的值;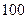 厘米的人数是
厘米的人数是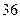 ,求出样本总量
,求出样本总量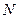 的数值;
的数值;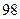 厘米并且小于
厘米并且小于 厘米学生数.
厘米学生数.