题目内容
(本小题满分12分)
已知函数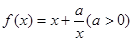 .
.
(1)判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)利用题(1)的结论,,求使不等式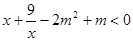 在
在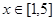 上恒成立时的实数
上恒成立时的实数 的取值范围?
的取值范围?
(1) 在
在 ,
,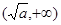 上是增函数,在
上是增函数,在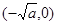 ,
,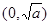 上是减函数.
上是减函数.
(2)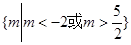 .
.
解析试题分析:(1)法一:用单调性定义可解.
法二: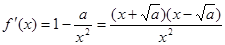 ,
,
当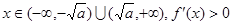 ;
;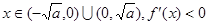 .……4分
.……4分
所以 在
在 ,
,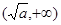 上是增函数,在
上是增函数,在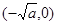 ,
,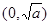 上是减函数.…5分
上是减函数.…5分
(2)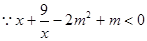 在
在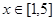 上恒成立,
上恒成立, 在
在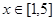 上恒成立,
上恒成立,
由(1)中结论可知,函数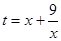 在
在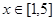 上的最大值为10,此时
上的最大值为10,此时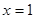 .
.
要使原命题成立,当且仅当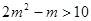 ,
,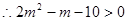 ,解得
,解得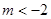 或
或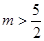 ,…11分
,…11分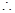 实数
实数 的取值范围是
的取值范围是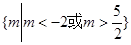 .
.
考点:本题主要考查应用导数研究函数的单调性及极值,简单不等式解法。
点评:典型题,本题属于导数应用中的基本问题,(2)作为 “恒成立问题”,转化成求函数最值问题。由本题看“对号函数”的性质值得关注。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
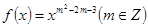 为偶函数,且在区间
为偶函数,且在区间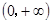 上是单调减函数(Ⅰ)求函数
上是单调减函数(Ⅰ)求函数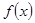 ;(Ⅱ)讨论
;(Ⅱ)讨论 的奇偶性.
的奇偶性.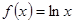 ,
,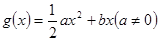
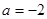 时,
时,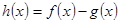 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象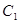 与函数
与函数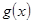 的图象
的图象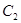 交于
交于 ,
,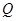 两点,过线段
两点,过线段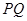 的中点
的中点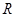 作
作 轴的垂线分别交
轴的垂线分别交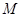 ,
,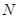 ,问是否存在点
,问是否存在点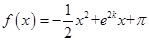 在
在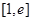 上具有单调性,求实数
上具有单调性,求实数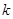 的取值范围;
的取值范围; 、
、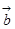 、
、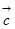 两两所成的角相等,且
两两所成的角相等,且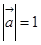 ,
,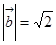 ,
,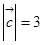 ,求
,求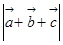 .
.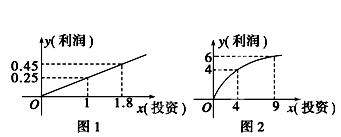
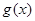 与
与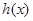 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式; ,且
,且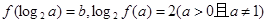 ,
,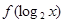 的最小值及相应 x的值;
的最小值及相应 x的值;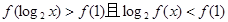 ,求x的取值范围.
,求x的取值范围.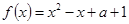
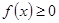 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数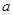 的取值范围.
的取值范围.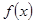 在区间
在区间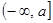 上的最小值
上的最小值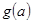 的表达式.
的表达式.