题目内容
设二次函数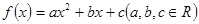 满足下列条件:①当
满足下列条件:①当 时,
时, 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线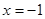 对称;②当
对称;②当 时,
时, 恒成立.
恒成立.
(1)求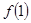 的值;
的值;
(2)求 的解析式;
的解析式;
(3)若 在区间
在区间 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.
(1)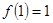 (2)
(2) (3)
(3)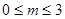
解析试题分析:(1)在②中令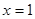 ,有
,有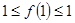 ,故
,故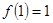 . 4分
. 4分
(2)当 时,
时, 的最小值为
的最小值为 且二次函数关于直线
且二次函数关于直线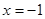 对称,
对称,
故设此二次函数为 . 6分
. 6分
因为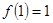 ,得
,得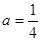 . 8分
. 8分
所以 . 10分
. 10分
(3)记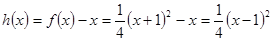 ,
,
显然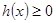 ,
, 在区间
在区间 上恒有
上恒有 ,即
,即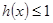 , 12分
, 12分
令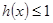 ,得
,得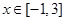 ,由
,由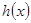 的图像只须
的图像只须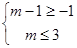 , 15分
, 15分
解得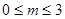 . 16分
. 16分
考点:本小题主要考查二次函数的图象和性质及恒成立问题.
点评:二次函数是高中学习中比较重要的一类函数,要准确掌握,灵活求解;恒成立问题一般转化为最值问题解决,这是经常考查的题型.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将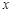 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
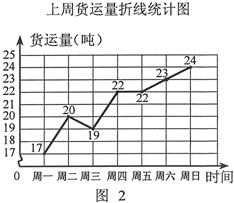
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
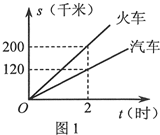
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与 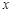 的函数关系式(不必写出
的函数关系式(不必写出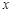 的取值范围),及
的取值范围),及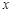 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
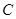 (单位:万元)与日产量
(单位:万元)与日产量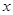 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式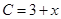 ,每日的销售额
,每日的销售额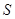 (单位:万元)与日产量
(单位:万元)与日产量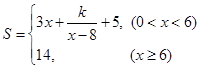
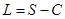 ,且当
,且当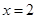 时,
时,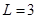 .
.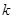 的值;
的值;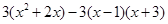
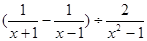
 元(
元(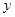 元.(14分)
元.(14分)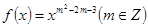 为偶函数,且在区间
为偶函数,且在区间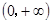 上是单调减函数(Ⅰ)求函数
上是单调减函数(Ⅰ)求函数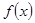 ;(Ⅱ)讨论
;(Ⅱ)讨论 的奇偶性.
的奇偶性.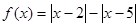 .
.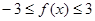 ;
;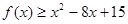 的解集.
的解集.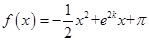 在
在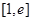 上具有单调性,求实数
上具有单调性,求实数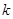 的取值范围;
的取值范围; 、
、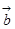 、
、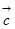 两两所成的角相等,且
两两所成的角相等,且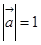 ,
,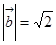 ,
,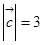 ,求
,求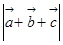 .
.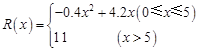 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: