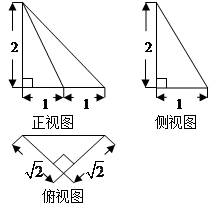题目内容
(本小题满分12分) 在三棱柱 中,底面是边长为
中,底面是边长为 的正三角形,点
的正三角形,点 在底面
在底面 上的射影
上的射影 恰是
恰是 中点.
中点.
(Ⅰ)求证: ;
;
(Ⅱ)当侧棱 和底面成
和底面成 角时, 求
角时, 求
(Ⅲ)若 为侧棱
为侧棱 上一点,当
上一点,当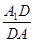 为何值时,
为何值时, .
.
 中,底面是边长为
中,底面是边长为 的正三角形,点
的正三角形,点 在底面
在底面 上的射影
上的射影 恰是
恰是 中点.
中点.(Ⅰ)求证:
 ;
;(Ⅱ)当侧棱
 和底面成
和底面成 角时, 求
角时, 求
(Ⅲ)若
 为侧棱
为侧棱 上一点,当
上一点,当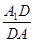 为何值时,
为何值时, .
.
(Ⅰ)见解析
(Ⅱ)
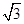
(Ⅲ)
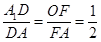
本试题主要考查了同学们的空间想象能力和逻辑推理能力及计算能力的综合运用。对于空间中点线面的位置关系的研究和灵活的运用。
(1)中利用线面垂直的性质定理得到
(2)中,分析棱锥的底面积和高度,可以得到体积。
(3)中,结合三垂线定理和中心的位置关系得到结论。
解法一:(Ⅰ)连结AO,∵A1O⊥面ABC,AO⊥BC.∴A1A⊥BC.
(Ⅱ)由(Ⅰ)得∠A1AO=45° 3分
由底面是边长为2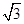 的正三角形,可知AO=3
的正三角形,可知AO=3
∴A1O=3,AA1=3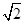
 4
4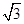 7分
7分
(Ⅲ)过D作DF∥A1O,交AO于F,则DF⊥平面ABC.
∴BF为BD在面ABC内的射影,
又∵A1C1∥AC,∴要使BD⊥A1C1,只要BD⊥AC,即证BF⊥AC,
∴F为△ABC的中心,∴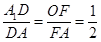 12分
12分
(1)中利用线面垂直的性质定理得到
(2)中,分析棱锥的底面积和高度,可以得到体积。
(3)中,结合三垂线定理和中心的位置关系得到结论。
解法一:(Ⅰ)连结AO,∵A1O⊥面ABC,AO⊥BC.∴A1A⊥BC.
(Ⅱ)由(Ⅰ)得∠A1AO=45° 3分
由底面是边长为2
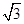 的正三角形,可知AO=3
的正三角形,可知AO=3∴A1O=3,AA1=3
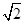
 4
4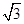 7分
7分(Ⅲ)过D作DF∥A1O,交AO于F,则DF⊥平面ABC.
∴BF为BD在面ABC内的射影,
又∵A1C1∥AC,∴要使BD⊥A1C1,只要BD⊥AC,即证BF⊥AC,
∴F为△ABC的中心,∴
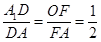 12分
12分
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
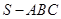 中,已知点
中,已知点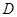 、
、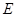 、
、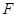 分别为棱
分别为棱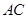 、
、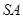 、
、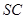 的中点
的中点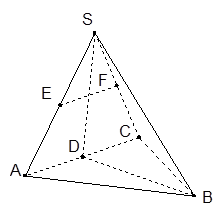
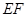 ∥平面
∥平面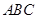
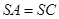 ,
,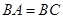 ,求证:平面
,求证:平面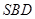 ⊥平面
⊥平面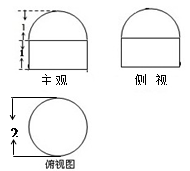




 是水平放置的一个平面图形的直观图,其中
是水平放置的一个平面图形的直观图,其中 ,
,  ,则原图形的面积为 。
,则原图形的面积为 。