题目内容
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
A.2 B.4 C.8 D.16
【答案】
B
【解析】
试题分析:由等差中项的定义得到关于a、b的关系式,再根据均值不等式化简即可得到关于a、b的等比中项的不等式,即可求最大值。
∵a、b的等差中项为4,∴a+b=8,又∵a、b是正数,∴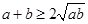 (a=b时等号成立)
(a=b时等号成立)
∴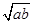 ≤4,又由等比中项的定义知a、b的等比中项为±
≤4,又由等比中项的定义知a、b的等比中项为±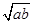 ∴a、b的等比中项的最大值为4,故选B
∴a、b的等比中项的最大值为4,故选B
考点:等差中项,等比中项
点评:本题考查等差中项和等比中项的定义和均值不等式,要注意两个数的等比中项有两个,同时要注意均值不等式的条件.属简单题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知两个正数a、b的等差中项是5,则a2、b2的等比中项的最大值为( )
| A、100 | B、50 | C、25 | D、10 |
已知两个正数a、b的等差中项为5,等比中项为4,则双曲线
-
=1的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|