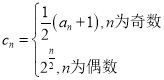题目内容
【题目】已知矩形
，
，
，将
沿对角线
进行翻折，得到三棱锥
，则在翻折的过程中，有下列结论：
①三棱锥的体积最大值为
；
②三棱锥的外接球体积不变；
③三棱锥的体积最大值时，二面角
的大小是
；
④异面直线
与
所成角的最大值为
.
其中正确的是（ ）
A.①②④B.②③C.②④D.③④
【答案】C
【解析】
考虑在翻折的过程中，当面ACD⊥面ACB时，D到底面的距离最大，进而得到棱锥体积最大，可判断①；取AC的中点O，可得O为棱锥的外接球的球心，计算可判断②；由①的解析过程知，三棱锥
的体积最大值时，平面
平面
，可判断③
假设AB⊥CD，由线面垂直的判断和性质，可判断④．
①
，当平面平面时，三棱锥的高最大，此时体积最大值为
，①错误；
②设
的中点为
，则由
，
知，
，所以为三棱锥外接球的球心，其半径为
，所以外接球体积为
，即三棱锥的外接球体积不变，②正确；
③由①的解析过程知，三棱锥的体积最大值时，平面平面，所以二面角
的大小是
，③错误；
④当
沿对角线进行翻折到使点
与点
的距离为
，即
时，在
中，
，所以
，又
，翻折后此垂直关系没有变，所以
平面
，所以
，即异面直线
与
所成角的最大值为，④正确.
故选C.
练习册系列答案
相关题目
