题目内容
已知双曲线C:| x2 |
| 9 |
| y2 |
| 16 |
| PF2 |
| F1F2 |
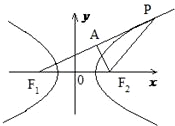
分析:先根据双曲线方程求出焦点坐标,再利用双曲线的性质求得|PF1|,作PF1边上的高AF2则可知AF1的长度,进而利用勾股定理求得AF2,则△PF1F2的面积可得.
解答:解:∵双曲线 C:
-
=1中a=3,b=4,c=5,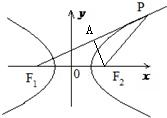
∴F1(-5,0),F2(5,0)
∵|PF2|=|F1F2|,
∴|PF1|=2a+|PF2|=6+10=16
作PF1边上的高AF2,则AF1=8,
∴|AF2|=
=6
∴△PF1F2的面积为S=
|PF1|•|AF2|=
×16×6=48
故答案为:48.
| x2 |
| 9 |
| y2 |
| 16 |

∴F1(-5,0),F2(5,0)
∵|PF2|=|F1F2|,
∴|PF1|=2a+|PF2|=6+10=16
作PF1边上的高AF2,则AF1=8,
∴|AF2|=
| 102-82 |
∴△PF1F2的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:48.
点评:此题重点考查双曲线的第一定义,双曲线中与焦点,准线有关三角形问题;由题意准确画出图象,利用数形结合,注意到三角形的特殊性.

练习册系列答案
相关题目
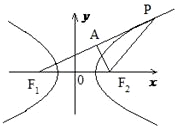 已知双曲线C:
已知双曲线C: