题目内容
(2013•南京二模)在平面直角坐标系xOy中,设过原点的直线l与圆C:(x-3)2+(y-1)2=4交于M、N两点,若MN≥2
,则直线l的斜率k的取值范围是
| 3 |
[0,
]
| 3 |
| 4 |
[0,
]
.| 3 |
| 4 |
分析:如图所示,过点C作OE⊥MN,垂足为E,连接CM.由|MN|≥2
,则可得|CE|≤
,利用点到直线的距离公式求出|CE|即可.
| 3 |
r2-(
|
解答:解:如图所示, 过点C作OE⊥MN,垂足为E,连接CM.
过点C作OE⊥MN,垂足为E,连接CM.
设直线MN的方程为y=kx,则|CE|=
=
,
∵|MN|≥2
,∴
≤
,
化为4k2-3k≤0,解得0≤k≤
.
故直线l的斜率k的取值范围是[0,
].
故答案为[0,
].
 过点C作OE⊥MN,垂足为E,连接CM.
过点C作OE⊥MN,垂足为E,连接CM.设直线MN的方程为y=kx,则|CE|=
r2-(
|
| |3k-1| | ||
|
∵|MN|≥2
| 3 |
| |3k-1| | ||
|
4-(
|
化为4k2-3k≤0,解得0≤k≤
| 3 |
| 4 |
故直线l的斜率k的取值范围是[0,
| 3 |
| 4 |
故答案为[0,
| 3 |
| 4 |
点评:熟练掌握直线与圆相交时弦长l、半径r及弦心距d三者之间的关系d2+(
l)2=r2及点到直线的距离公式是解题的关键.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
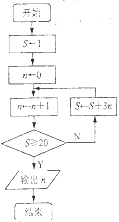 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是