题目内容

6．设等差数列{an}的前n项和为Sn，已知S10=100，则a2+a9=（　　）
A．100B．40C．20D．12

分析 由题意和等差数列的前n项和公式求出a1+a10，根据等差数列的性质求出a2+a9的值．

解答 解：∵S10=100，∴$\frac{10（{a}_{1}+{a}_{10}）}{2}$=100，解得a1+a10=20，
由等差数列的性质得，a2+a9=a1+a10=20，
故选：C．

点评 本题考查等差数列的前n项和公式，以及等差数列的性质的灵活应用，属于中档题．

练习册系列答案
相关题目
16．△ABC的顶点为A（4，0），B（0，4），C（0，0），则△ABC的内切圆圆心的横坐标是（　　）
A．2$\sqrt{2}$-4B．4-2$\sqrt{2}$C．4+2$\sqrt{2}$D．4
17．执行程序框图，如果输入a=2，那么输出n=（　　）
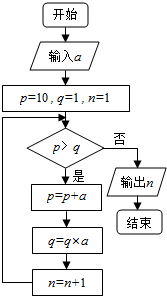
A．3B．4C．5D．6
14．设变量x，y满足不等式组：$\left\{\begin{array}{l}{y≥x}\\{x+3y≤3}\\{x≥-3}\end{array}\right.$，则z=x+y的最小值为（　　）
A．-9B．-6C．-1D．$\frac{3}{2}$
1．抛物线y2=2px（p＞0）上一点M（1，m）（m＞0）到其焦点F的距离为4，则△OMF（O为原点）的面积为3$\sqrt{3}$．
11．等差数列{an}的前n项和为Sn，已知a1=13，a2为整数，且Sn≤S5．
（1）求{an}的通项公式；
（2）设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{bn}的前n项和Tn．
18．已知函数y=cosx与y=sin（2x+φ）（0≤φ＜π），它们的图象有一个横坐标为$\frac{π}{3}$的交点，则φ=（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
15．观察下列等式

照此规律下去
（Ⅰ）写出第5个等式；
（Ⅱ）你能做出什么一般性的猜想？请用数学归纳法证明猜想．
16．已知函数f（x）=$\left\{\begin{array}{l}\frac{1}{x}，x＞0\\{3^x}，x≤0\end{array}$，则f（f（-2））=（　　）
A．$\frac{1}{9}$B．$\frac{{\sqrt{3}}}{3}$C．$\sqrt{3}$D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网