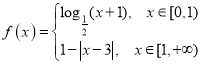题目内容
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如表:
月收入(单位百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(Ⅰ)由以上统计数据填下面2×2列联表并问是否有99%的把握认为“月收入以5500为分界点”对“楼市限购令”的态度有差异;
月收入低于55百元的人数 | 月收入不低于55百元的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若采用分层抽样在月收入在[15,25),[25,35)的被调查人中共随机抽取6人进行追踪调查,并给予其中3人“红包”奖励,求收到“红包”奖励的3人中至少有1人收入在[15,25)的概率.
参考公式:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(Ⅰ)填表见解析,没有 (Ⅱ)![]()
【解析】
(Ⅰ)由题意填表,计算K2,对照临界值得出结论 (Ⅱ)由分层抽样求出抽取的人数,列举法写出基本事件,计算概率即可.
(Ⅰ)由题意填2×2列联表如下,
月收入低于55百元的人数 | 月收入不低于55百元的人数 | 合计 | |
赞成 | 29 | 3 | 32 |
不赞成 | 11 | 7 | 18 |
合计 | 40 | 10 | 50 |
由表中数据,计算K2![]() 6.27<6.635,
6.27<6.635,
所以没有99%的把握认为“月收入以5500为分界点”对“楼市限购令”的态度有差异;
(Ⅱ)用分层抽样在月收入在[15,25),[25,35)的被调查人中随机抽取6人,则月收入在[15,25)内有6![]() 2(人)记为AB,在[25,35)有6﹣2=4(人),记为cdef;
2(人)记为AB,在[25,35)有6﹣2=4(人),记为cdef;
从这6人中抽取3人,基本事件是ABcABdABeABfAcdAceAcfAdeAdfAefBcdBceBcfBdeBdfBefcdecdfcefdef共20种,
这3人中至少收入在[15,25)的事件是ABcABdABeABfAcdAceAcfAdeAdfAefBcdBceBcfBdeBdfBef共16种,
故所求的概率值为P![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案