题目内容
【题目】设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,动点P满足
,动点P满足![]() ,设动点P的轨迹为
,设动点P的轨迹为![]() ,以动点P到点
,以动点P到点![]() 距离的最大值为长轴,以点
距离的最大值为长轴,以点![]() 、
、![]() 为左、右焦点的椭圆为
为左、右焦点的椭圆为![]() ,则曲线
,则曲线![]() 和曲线
和曲线![]() 的交点到
的交点到![]() 轴的距离为_________.
轴的距离为_________.
【答案】![]()
【解析】
由动点P满足![]() ,则可得到动点
,则可得到动点![]() 在以线段
在以线段![]() 为弦的圆上,由圆的性质可得圆心
为弦的圆上,由圆的性质可得圆心![]() 为
为![]() 或
或![]() ,半径为2,则动点P到点
,半径为2,则动点P到点![]() 距离的最大值为4,即可得到椭圆的方程,联立部分曲线
距离的最大值为4,即可得到椭圆的方程,联立部分曲线![]() 的方程与椭圆方程求解即可
的方程与椭圆方程求解即可
由题,因为动点P满足![]() ,则动点
,则动点![]() 在以线段
在以线段![]() 为弦的圆上,
为弦的圆上,
因为点![]() 、
、![]() 关于
关于![]() 轴对称,则圆心在
轴对称,则圆心在![]() 轴上,设圆心为
轴上,设圆心为![]() ,原点为
,原点为![]() ,
,
因为![]() ,所以
,所以![]() ,则在
,则在![]() 中,
中,![]() ,所以
,所以![]() ,
,![]() ,则圆心
,则圆心![]() 为
为![]() 或
或![]() ,
,
当![]() 时, 曲线
时, 曲线![]() 的方程为
的方程为![]() ;当
;当![]() 时, 曲线
时, 曲线![]() 的方程为
的方程为![]() ;显然,曲线
;显然,曲线![]() 关于
关于![]() 轴对称,
轴对称,
所以动点P到点![]() 距离的最大值为圆的直径,即
距离的最大值为圆的直径,即![]() ,则长轴长为4,
,则长轴长为4,
所以椭圆![]() 为
为![]() ,
,
则曲线![]() 与曲线
与曲线![]() 的图象如下图所示:
的图象如下图所示:
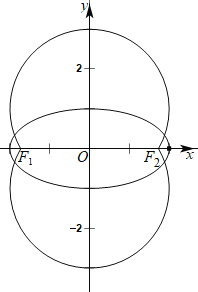
因为曲线![]() 与曲线
与曲线![]() 均关于
均关于![]() 轴对称,所以可只考虑
轴对称,所以可只考虑![]() 轴上方形成的交点,
轴上方形成的交点,
即联立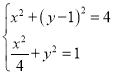 ,消去
,消去![]() 得,
得,![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
故曲线![]() 和曲线
和曲线![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,
,
故答案为:![]()

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目