题目内容
5.等差数列{an}中,前n项和为Sn,|a3|=|a9|,公差d<0.若存自然数N,对于任意的自然数n≥N,总有Sn+1≤Sn成立,则N值为( )| A. | 7和8 | B. | 6和7 | C. | 5和6 | D. | 4和5 |
分析 根据题意,求出首项a1与公差d的关系,得出通项公式an,利用Sn+1≤Sn,得出$\left\{\begin{array}{l}{{a}_{n}≥0}\\{{a}_{n+1}≤0}\end{array}\right.$,由此求出n的值.
解答 解:等差数列中,∵|a3|=|a9|,
∴a32=a92,
即(a1+2d)2=(a1+8d)2,
∴a1=-5d,
∴an=a1+(n-1)d=(n-6)d;
又Sn+1≤Sn,
∴$\left\{\begin{array}{l}{{a}_{n}≥0}\\{{a}_{n+1}≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{(n-6)d≥0}\\{(n+1-6)d≤0}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{n-6≤0}\\{n-5≥0}\end{array}\right.$,
解得5≤n≤6.
故选:C.
点评 本题考查了等差数列的前n项和以及灵活运用等差数列的通项公式解决问题的能力,是中档题目.

练习册系列答案
相关题目
13.执行如图所示的程序框图,则输出的S的值为( )


| A. | 1023 | B. | 1024 | C. | 2047 | D. | 2048 |
10.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值为2,则a的值为( )
| A. | 2 | B. | -1或-3 | C. | 2或-3 | D. | -1或2 |
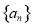 ,
,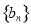 都是等差数列,若
都是等差数列,若 ,则
,则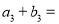 _____________.
_____________. 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: