题目内容
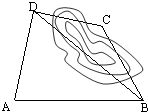 (2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).
(2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).参考数据:
| 2 |
| 3 |
| 5 |
分析:利用余弦定理求出BD,再用正弦定理求BC即可.
解答: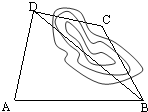 解:在△ABD中,设BD=x,则BA2=BD2+AD2-2BD•AD•cos∠BDA,
解:在△ABD中,设BD=x,则BA2=BD2+AD2-2BD•AD•cos∠BDA,
即142=x2+102-2•10x•cos60°,
整理得:x2-10x-96=0,
解之:x1=16,x2=-6(舍去),
由正弦定理,得:
=
所以BC=
•sin30°=8
≈11.3(km)
 解:在△ABD中,设BD=x,则BA2=BD2+AD2-2BD•AD•cos∠BDA,
解:在△ABD中,设BD=x,则BA2=BD2+AD2-2BD•AD•cos∠BDA,即142=x2+102-2•10x•cos60°,
整理得:x2-10x-96=0,
解之:x1=16,x2=-6(舍去),
由正弦定理,得:
| BC |
| sin∠CDB |
| BD |
| sin∠BCD |
所以BC=
| 16 |
| sin135° |
| 2 |
点评:本题考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
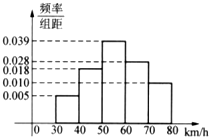 (2007•汕头二模)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
(2007•汕头二模)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )